Урок 51

Тема. Решение задач

Цель урока: формирование умений учащихся применять изученный материал к решению задач.

Оборудование: схемы «Расстояние между двумя точками», «Координаты середины отрезка», «Преобразование фигур».

Ход урока

И. Проверка домашнего задания

Коллективное обсуждение контрольных вопросов № 12-13 и решение задачи № 28.

1. Даны координаты четырех вершин куба ABCDA1B1C1D1: А(0;0;0), B(0;0;1), D(0;1;0), A,(1;0;0). Найдите координаты последних вершин куба.

(Ответ. В1 (1;0;1), C(0;1;1), C1(1;1;1), D1(1;1;0))

2. Дано точки А (-4; 7; 0) и В(0; -1; 2). Найдите расстояние от начала координат до середины отрезка АВ. (Ответ. )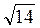

3. Лежат ли точки А, В, С на одной прямой, если:

а) А(0;12;17), В(9;-3;8). С(18; -18; -1);

б) А(6;18;8), В(7;9;17), С(8;0;-6)?

(Ответ а) Да; б) нет.)

4. Определите вид треугольника АВС, если:

а) А(7;1;-7), В(0;8;-7), С(0;1;0);

б) А(0;-10;-6), В(0;-8;-6), С(-1;-8;-5);

в) А(-5;2;1), В(-4;2;1), С(-5;3;1).

(Ответ а) Правильный; б) прямоугольный разносторонний;

в) прямоугольный равнобедренный.)

5. Найти координаты точки, которая лежит на оси у и равноудалена от точек А (4;-1; 3) и B(1;3;0). (Ответ. (0; - 2; 0).)

6. Найти координаты вершины D параллелограмма ABCD, если А (1; 3; 2), В(0;2;4), C(1;1;4). (Ответ. D (2; 2; 2).)

III. Домашнее задание

Подготовиться к тематической аттестации № 5. Решить задачи№ 10 (2), 11 (2), 14, 25 (3) (с. 55-56).

В ходе беседы выяснить, что нового изучены в данной теме.