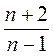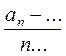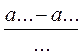УРОК № 51
Тема. Арифметическая прогрессия. Формула n-го члена арифметической прогрессии
Цель урока: закрепить знания учащихся о содержании определения и сопутствующих понятий арифметической прогрессии, а также о ее основных свойства. Дополнить эти знания знанием формулы n-го члена арифметической прогрессии.
Закрепить умения: находить арифметическую прогрессию среди числовых последовательностей, находить разность арифметической прогрессии, первые члены арифметической прогрессии, а также использовать свойства арифметической прогрессии. Сформировать умение записывать формулу n-го члена арифметической прогрессии, а также решать различные по содержанию задачи на применение этой формулы.
Тип урока: дополнение и закрепление знаний, отработка умений и навыков.
Наглядность и оборудование: опорный конспект № 30.
Ход урока
И. Организационный этап
Учитель проверяет готовность учащихся к уроку, настраивает их на работу.
II. Проверка домашнего задания
Для осознанной работы учащихся на этом этапе урока можно провести проверку домашнего задания по образцу.
Другой вариант проведения этого этапа урока - выполнение тестовых заданий (см. ниже) с последующей проверкой и обсуждением результатов их выполнения, что позволит повторить содержание основных понятий предыдущего урока, а также схемы применения изученных на этом уроке понятий для решения типовых задач.
Тестовые задания
1. 1. Какая из следующих последовательностей является арифметической прогрессией?
а) 1; 3; 5; 8;
б) 10; 7; 4; 1;
в) 2; 6; 11; 15;
г) 4; -5; 6; -7.
2. Первый член арифметической прогрессии равен 3, а разность 2. Чему равен второй член этой прогрессии?
а) 7; б) 9; в) -1; г) 5.
3. Найдите разность арифметической прогрессии (аn), если а2 = 3, а3 = -3.
а) -2; б) -6; в) 2; г) 6.
4. Чему равна разность арифметической прогрессии (аn), если а2 = 4, а4 = 28.
а) -12; б) 12; в) 4; г) 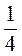 .
.
III. Формулировка цели и задач урока.
Мотивация учебной деятельности учащихся
Для осознания учащимися необходимости изучения формулы п-го члена арифметической прогрессии и дальнейшего ее применения можно предложить им выполнить такое упражнение: зная первый член и разность арифметической прогрессии, найти ее некоторое член (номер которого есть достаточно большим). Осознав нерациональность решения задачи известным ученикам способом (через применение рекуррентной формулы), они приходят к вопросу: не существует способа нахождения любого члена арифметической прогрессии без необходимости находить предыдущие несколько ее членов? Поиск ответа на этот вопрос - основная цель урока.
IV. Актуализация опорных знаний и умений учащихся
Устные упражнения
1. Данная конечная последовательность: 2; -1; -4; -7; -10; -13.
1) Проверьте, является ли эта последовательность арифметической прогрессией.
2) Назовите ее первый член и разность.
3) Задайте ее рекурентною формуле.
4) Продолжите ее еще тремя числами, которые вместе с данными образовали бы арифметическую прогрессию.
2. Какая из данных последовательностей (хп) представляет собой арифметическую прогрессию:
1) хn = 2n + 5;
2) хn = 3n2 + 6n;
3) хn = 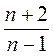 ?
?
Для арифметической прогрессии найдите первые три члена и разницу.
V. Дополнение знаний
План изучения нового материала
1. Формула n-го члена арифметической прогрессии.
2. Примеры применение выведенной формулы.
Опорный конспект № 30
Формула n-го члена арифметической прогрессии |
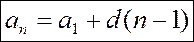
где an - n-й член арифметической прогрессии;
а1 - первый член арифметической прогрессии;
d - разность арифметической прогрессии;
n - номер члена арифметической прогрессии. |
Пример. Найдем а9, если (аn) - арифметическая прогрессия, первые члены которой: 7,8; 8,9; 10; ....
Решение
Найдем разность арифметической прогрессии, у которой а1 = 7,8; a2 = 8,9; a3 = 10: d = a3 - a2 = 10 - 8,9 = 1,1.
Формула n-го члена арифметической прогрессии имеет вид an = a1 + d(n - 1).
Учитывая, что а1 = 7,8, d = 1,1, имеем: аn = 7,8 + 1,1(n - 1).
Итак, а9= 7,8 + 1,1(9 - 1) = 7,8 + 8,8 = 16,6.
Ответ: а9 = 16,6. |
Методический комментарий
Единственный новый момент, который прилагается к изученных на предыдущем уроке определение и свойства арифметической прогрессии,- это формула п-го члена арифметической прогрессии, которая выводится через определение и сама в дальнейшем будет основой для вывода формулы суммы п первых членов арифметической прогрессии. Как процесс получения этой формулы, так и способы ее применения для решения задач, а также ситуации, в которых эта формула «работает», не изменились по сравнению с предыдущими годами. Примерное содержание учебного материала помещен в опорный конспект № 30.
VI. Отработка умений
Устные упражнения
1. Найдите а1 и d по формуле п-го члена арифметической прогрессии (аn):
1) аn = 1 + 3(n - 1);
2) аn = 0,1 - 3(n - 1).
2. Запишите формулу первого члена арифметической прогрессии, в которой:
1) а1 = 2; d = -3;
2) а1 = 0,5; d = 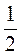 ;
;
3) а1 = -0,2; d = -2.
3. Для некоторой арифметической прогрессии запишите формулу ее 10-го члена; 21 члена; n + 1 члена.
Письменные упражнения
Содержание письменных упражнений урока может быть таким:
1) задачи на прямое применение формулы n-го члена арифметической прогрессии, у которой задан первый член и разность или которая задана перечнем первых нескольких своих членов;
2) найти п-й член, если известны несколько первых членов арифметической прогрессии;
3) найти номер некоторого члена арифметической прогрессии или проверить, является ли данное число членом арифметической прогрессии;
4) прикладные задачи на применение определение арифметической прогрессии и формулу ее n-го члена.
Методический комментарий
Содержание упражнений и цель, которой добивается учитель при решение этих упражнений, такие же, как и на предыдущем уроке: закрепление определения и формулы, изученных на этих уроках, а также выработки оперативных умений применения формул при решении задач в различных ситуациях. (Если позволяют успехи учащихся, повышается уровень сложности задач за счет задач на применение свойств арифметической прогрессии.)
VI. Итоги урока
Контрольные вопросы
1. Какой вид имеет формула п-го члена арифметической прогрессии, у которой: 1) bn членов; 2) хn членов.
2. Известно, что (аn) - арифметическая прогрессия. Заполните пропуски так, чтобы равенства стали верными:
1) an =... + d ...;
2) d = 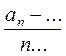 ;
;
3) а1 = ап - ...(n - 1);
4) n = 1 + 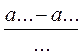 .
.
VII. Домашнее задание
1. Изучить содержание материала с опорными конспектами № 29, 30.
2. Выполнить самостоятельную работу (см. ниже) с вариантом, указанным учителем.
Самостоятельная работа
Вариант 1
Решите задачи.
1. Найдите первые четыре члена арифметической прогрессии (аn), если а1 = 1,2, d = -0,1.
2. Найдите разницу и сотый член арифметической прогрессии (аn): 2,7; 3,1; 3,5; ... .
3. Между числами -4 и 5 вставьте пять таких чисел, чтобы они вместе с данными числами образовали арифметическую прогрессию.
4. Дана арифметическая прогрессия: 2; 1,8; 1,6; ... . Найдите наибольший отрицательный член.
Вариант 2
Решите задачи.
1. Найдите первые четыре члена арифметической прогрессии (аn), если a1 = -1,2, d = 0,3.
2. Найдите разницу и сотый член арифметической прогрессии (аn): 5,4; 4,8; 4,2; ... .
3. Между числами -3 и 11 вставьте шесть таких чисел, чтобы они вместе с данными числами образовали арифметическую прогрессию.
4. Дана арифметическая прогрессия: -3,6; -3,3; -3; ... . Найдите ее наименьший положительный член.