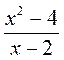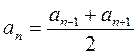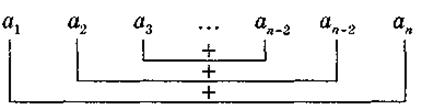УРОК № 50
Тема. Арифметическая прогрессия. Формула n-го члена арифметической прогрессии
Цель урока: добиться усвоения учащимися: определение арифметической прогрессии, соответствующей терминологии (разность арифметической прогрессии); рекуррентной формулы и основных свойств арифметической прогрессии (включая характеристическую свойство).
Выработать умения: воспроизводить содержание изученных понятий, а также использовать их для решения задач, предусматривающих выделение арифметической прогрессии среди других числовых последовательностей, использование рекуррентной формулы арифметической прогрессии, а также использования ее свойств.
Тип урока: усвоение знаний, выработка умений.
Наглядность и оборудование: опорный конспект № 29.
Ход урока
I. Организационный этап
Учитель проверяет готовность учащихся к уроку, настраивает их на работу.
II. Проверка домашнего задания
Для выяснения уровня усвоения учащимися содержания понятий предыдущего урока учитель предлагает им выполнить тестовые задания [9, тест 19] с последующей проверкой и коррекцией.
III. Формулировка цели и задач урока.
Мотивация учебной деятельности учащихся
Для осознания учащимися необходимости выделения и дальнейшего изучения свойств последовательностей, вынесенных в тему урока, можно предложить им выполнить упражнение на сравнение или логическую упражнение на исключение лишнего.
После выполнения таких упражнений учащиеся осознают, что среди бесконечного количества различных по видам числовых последовательностей, кроме названных в предыдущем уроке видов, можно выделить (по другим критериям) другие виды. Среди них особняком стоят последовательности, в которых последующий член равен предыдущему члену, который того же числа. После такого умозаключения формулируется основная дидактическая цель урока: изучить определение, дать ему название и исследовать свойства таких последовательностей и их применение.
IV. Актуализация опорных знаний и умений учащихся
Устные упражнения
1. Дано конечную последовательность: (хn): 3; 0; -3; -6; -9; -12. Укажите:
1) первый, третий, шестой члены этой последовательности;
2) является ли эта последовательность возрастающей, убывающей;
3) формулу ее n-го члена.
2. Последовательность (аn) задана формулой аn = 3n - 1. Укажите:
1) а1, а2, а3;
2) номер члена, который равен 26;
3) является ли членом этой последовательности число 47; 58?
3. Решите уравнение:
1) 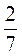 х =
х = 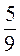 ;
;
2) х2 - 3х = 0;
3) х2 - 2х +1 = 0;
4) х2 - 3х - 4 = 0;
5) 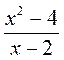 = 0.
= 0.
V. Формирование знаний
План изучения нового материала
1. Определение арифметической прогрессии. Разность арифметической прогрессии.
2. Рекуррентная формула арифметической прогрессии.
3. Свойства арифметической прогрессии:
1) характеристическая свойство арифметической прогрессии;
2) сумма членов конечной арифметической прогрессии, равноотстоящих от ее концов;
3)* теорема о задание арифметической прогрессии формулой an = kn + b, где k, b - некоторые числа.
Опорный конспект № 29
|
Арифметическая прогрессия - числовая последовательность, в которой каждый следующий член, начиная со второго, равен предыдущему члену, к которому прилагается то самое число. Это число называют разностью арифметической прогрессии. |
|
|
Пример. 1; 3; 5; 7; 9 - арифметическая прогрессия.
3 - 1 = 5 - 3 = 7 - 5 = 9 - 7 = 2; 2 - разность арифметической прогрессии. |
|
|
Рекуррентная формула арифметической прогрессии |
|
|
аn+1 = аn + d, d - разность арифметической прогрессии.
d = an+1 - n. |
|
|
|
|
Свойства арифметической прогрессии |
1. 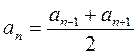 , где n >1 , где n >1
аn - n-й член арифметической прогрессии, является средним арифметическим двух соседних с ним членов. |
2. Если (аn) - арифметическая прогрессия (конечна), то: |
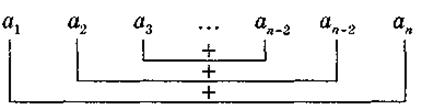
|
Сумма двух членов конечной арифметической прогрессии, равноотстоящих от ее концов, равна сумме крайних членов этой прогрессии. |
3. Теорема*. Любая арифметическая прогрессия (аn) может быть задана формулой an = kn + b, где k и b - некоторые числа; и наоборот, если последовательность (аn) задана формулой an = kn + b, где k и b - некоторые числа, то эта последовательность является арифметической прогрессией. |
Методический комментарий
Изучение материала урока начинается с формулировки определения арифметической прогрессии (ученики подготовлены к его восприятию на предыдущем этапе урока), в котором следует обратить внимание учащихся на словосочетание «начиная со второго», а также на то, что число, которое добавляется к каждого члена, начиная со второго, является постоянным для данной арифметической прогрессии, при этом оно может быть каким угодно (положительным или отрицательным; целым или дробным; оно может составлять даже 0; это желательно проиллюстрировать множеством примеров). После этого формулируется представление о содержании понятия «разность арифметической прогрессии» и записывается соответствующая формула. Далее традиционно записывается рекуррентная формула арифметической прогрессии, которая напрямую вытекает из определения арифметической прогрессии.
Для решения многих прикладных задач важными являются свойства арифметической прогрессии, в частности характеристическая свойство (хотя программа по математике не дает ее среди обязательных знаний в этой теме). Также не обязательным, однако интересной для применения является теорема о задание арифметической прогрессии формулой an = kn + b, где k, b - некоторые числа. Поэтому, если позволяют особенности класса, можно предложить названные свойства арифметической прогрессии рассмотреть как дополнительный материал.
VI. Формирование умений
Устные упражнения
1. Найдите третий член и разность арифметической прогрессии:
1) 2; 7; 12; ...;
2) 6; 5,5; 5; ...;
3) 0,7; 1; 1,3; ...;
4) -9; -7; -5; ... .
2. Найдите первые четыре члена арифметической прогрессии (аn), в которой:
1) a1 = 5, d = 2;
2) a1 = 7, d = -2.
3. Найдите четвертый член арифметической прогрессии:
1) 7; 11; 15; ...;
2) 13; 10; 7; ... .
4. Найдите пропущенный член арифметической прогрессии:
1) 1; 2; 7; а4; ...;
2) a1; 5; 3; ... .
Письменные упражнения
Для реализации дидактической цели урока следует решить задачи следующего содержания:
1) среди предложенных последовательностей выберите арифметические прогрессии;
2) указать п-й член и разность арифметической прогрессии, заданной перечнем ее первых членов;
3) за рекурентною формуле найти несколько первых членов арифметической прогрессии;
4) упражнения на использование свойств арифметической прогрессии;
5) на повторение: упражнения на решения рациональных уравнений.
Методический комментарий
При решении упражнений, кроме закрепления терминологии и формул, выражающих свойства, проводится отработка таких ключевых моментов: как проверить, является ли заданная последовательность арифметической прогрессией (по определению, или по характеристичной свойством, или по теореме, в зависимости от условия); как найти разность арифметической прогрессии (от любого члена, начиная со второго, вычесть предыдущий него член); как найти член, следующий за данным членом арифметической прогрессии (найти разность арифметической прогрессии и добавить ее к данному члену).
VII. Итоги урока
Контрольные вопросы
1. Что называется арифметической прогрессией? Приведите примеры.
2. Как найти разность арифметической прогрессии?
3. Сформулируйте свойства арифметической прогрессии.
VIII. Домашнее задание
1. Изучить определения понятий, рассмотренных на уроке (см. опорный конспект № 29).
2. Решить упражнения, аналогичные по содержанию и уровню сложности выполненной на уроке.
3. Повторить схему решения задач составлением математической модели.