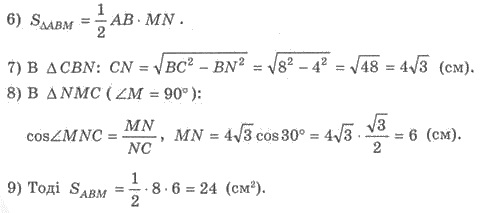ГЕОМЕТРИЯ

Раздел ІІ. СТЕРЕОМЕТРИЯ

§17. ПИРАМИДА.

3. Сечения пирамиды.

Рассмотрим простейший сечение пирамиды.

Сечение пирамиды, проходящее через два боковых ребра, не принадлежащих одной грани, называют диагональным сечением.

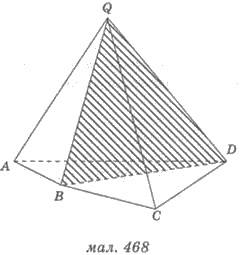
На рисунке 468: QВD - диагональный сечение четырехугольной пирамиды QАВСD.

Диагональные сечения пирамиды - треугольника, одной из вершин которых является вершина пирамиды, а противоположная ей сторона - диагональ основания.

Пример 1. Найти периметр диагонального сечения правильной четырехугольной пирамиды, сторона основания которой равна 3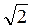 см, а боковое ребро - 5 см.

Решения. 1) Пусть QАВСD - правильная четырехугольная пирамида (рис. 467), QАС - ее диагональный разрез.

2) По условию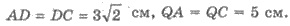

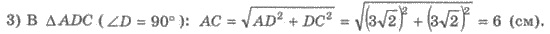
4) Тогда периметр сечения Г = 6 + 5 + 5 = 16 (см).

Часто в задачах рассматривают сечения пирамиды, проходящих через сторону основания пирамиды и пересекают боковые ребра пирамиды.

Пример 2. В правильной треугольной пирамиде, сторона основания которой равна 8 см, через сторону основания перпендикулярно бокового ребра проведено сечение. Найти площадь сечения, если он образует угол 30° с плоскостью основания пирамиды.

Решения. 1) Проведем в правильной пирамиде QABC с основанием ABC высоту ВМ боковой грани BQC (рис. 469).

2) ∆ВМС = ∆АМС (за двумя сторонами и углом между ними), поэтому АМС = BMC = 90°.

3) По признаку перпендикулярности прямой и плоскости: АМВ QC. Поэтому АВМ - сечение, площадь которого надо найти.

4) CN - высота основания пирамиды, CN АВ, поэтому по теореме о трех перпендикулярами MN АВ.

5) По признаку перпендикулярности прямой и плоскости имеем MNC АВ, поэтому угол MNC - угол, который образует сечение с плоскостью основы. По условию MNC = 30°.