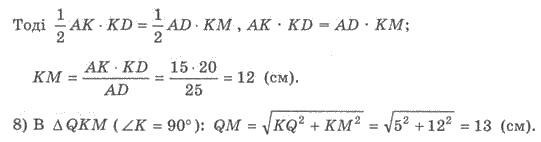ГЕОМЕТРИЯ

Раздел ІІ. СТЕРЕОМЕТРИЯ

§17. ПИРАМИДА.

1. Определение пирамиды. Элементы пирамиды.

Пирамидой называют многогранник, в которого одна из граней (которую называют основой) - произвольный многоугольник, остальные грани - треугольники с общей вершиной.

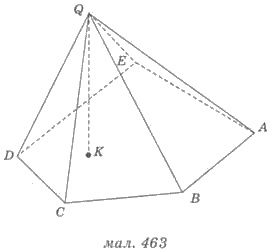
На рисунке 463 изображена пирамида, основой которой является многоугольник АВСDЕ. Грани с общей вершиной, о которые идет речь в указанные пирамиды - треугольники АВQ, ВСQ, СDQ, DЕQ, АЕQ. Эти грани называют боковыми гранями піраміди. их общую вершину - точку Q называют вершиной пирамиды. Пирамиду, изображенную на рисунке 463 называют пирамидой QАВСDЕ. Ребра пирамиды, соединяющие вершину пирамиды с вершинами основания пирамиды, называют боковыми ребрами пирамиды. На рисунке 463 отрезки QА QВ, QС, QD и QЕ - боковые ребра пирамиды.

Пирамиду называют n-угольной, если ее основанием является n-угольник.

Треугольную пирамиду называют также тетраэдр. На рисунке 463 изображен пятиугольную пирамиду.

Перпендикуляр, проведенный из вершины пирамиды к плоскости основания, называют высотой пирамиды.

На рисунке 463 отрезок Q)К является высотой пирамиды, точка К - основой высоты.

При решении задач важной является следующее свойство:

Если в пирамиде выполняется одна из двух следующих условий: все боковые ребра образуют с плоскостью основания равные углы или длины всех боковых ребер равны, то основанием высоты пирамиды является центр окружности описанного вокруг основания пирамиды.

Пример 1. Каждое из боковых ребер тетраэдра равен 65/8 см. Основанием пирамиды является треугольник со сторонами 5 см, 5 см и 6 см. Найти высоту пирамиды.

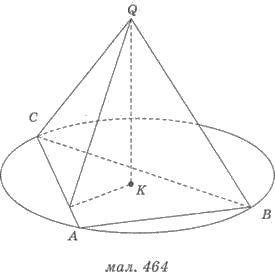
Решение (рис. 464). 1) Пусть QАВС - тетраэдр, что задано в условии, 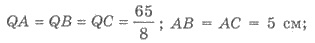ВС = 6 см; QК - высота тетраэдра.

2) Поскольку все боковые ребра тетраэдра равны, то точка К - центр круга, описанного вокруг #8710;АВС; АК = R - радиус круга, описанного вокруг этого треугольника.

3) По известной формуле 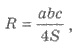где а, b, с - стороны треугольника; S - его площадь.

4) Найдем площадь треугольника по формуле Герона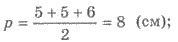

Также при решении задач важным является свойство:

Если в пирамиде выполняется одна из двух следующих условий: все боковые грани образуют с плоскостью основания равные углы или длины высот всех боковых граней равны, то основанием высоты пирамиды является центр круга, вписанного в основание пирамиды.

Пример 2. Основанием пирамиды является ромб с диагоналями 40 см и 30 см. Высота пирамиды равна 5 см. Все высоты боковых граней равны между собой. Найти длину высоты боковой грани.

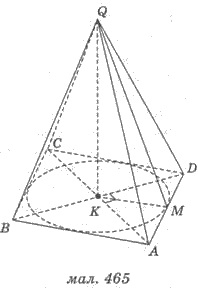
Решения. 1) Поскольку все высоты боковых граней равны между собой, то основанием высоты пирамиды является центр окружности, вписанного в основание. Поскольку основой является ромб, то точка К - основание высоты является точкой пересечения диагоналей ромба. На рисунке 465 изображена пирамида QАВСD, что задано в условии.

2) АВСD - основание пирамиды, АС = 30 см, ВD = 40 см, QК - высота пирамиды, QК = 5 см.

3) QМ - высота боковой грани, QМ АD

4) КМ - проекция Qна плоскость основания. По теореме о три перпендикуляры: КМ АD.

5) АD - высота прямоугольного треугольника АКD.

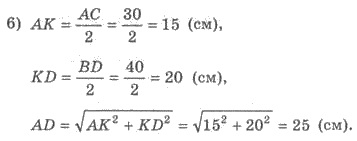
7) Найдем дважды площадь ∆АКD: