|
По окончании этой работы осуществляем самопроверку и коррекцию, повторив основные теоретические положения.
III. Формулировка цели и задач урока @ После проведенного II этапа урока, во время которого повторяются основные теоретические сведения, использованные на предыдущем уроке, большинство учеников осознает тот факт, что основной целью урока будет дальнейшая работа по выработке умений и отработка навыков использования в подобных ситуациях (разложении на множители) других изученных формул сокращенного умножения.
IV. Актуализация опорных знаний Работа с опережающим домашним заданием Выполнение устных упражнений 1. Представьте выражение в виде квадрата одночлена: 36; l6в2; 0,09t2; 2. Представьте выражение в виде куба одночлена: 27; 8х3; 3. Чему равна неполный квадрат суммы и неполный квадрат разности выражений: х и у; 3 и х; а 4. Прочитайте выражение, используя слова «сумма», «разность», «квадрат», «куб», «произведение»: a + b; a - b; a2 - b2; a2 + b2; а3 + b3; а3 - b3. Какие из этих выражений можно разложить на множители по формулам сокращенного умножения? Прочитайте эти формулы, используя выделенные слова.
V. Применение умений @ Эта группа формул (разность квадратов, сумма и разность кубов) является более простой для учеников. Но есть несколько моментов, на которые сразу стоит обратить внимание, чтобы предупредить возможные ошибки: 1) по разности квадратов: раскладывается по формуле разность квадратов и ни в коем случае не сумма (имеем в виду только множество действительных чисел); чтобы применить эту формулу, данное выражение сначала подаем как разность квадратов; 2) относительно суммы/разности кубов еще раз обращаем внимание на запись и следим, чтобы второй множитель был именно неполным квадратом разности/суммы.
Выполнение устных упражнений 1. Представьте выражение в виде разности квадратов двух выражений: 1) р2 - 4; 2) 16 - с2; 3) b2 - 1; 4) 4х2 - 25; 5) 49а2 - 9b2; 6) (m - 1)2 - 4. 2. Представьте выражение в виде суммы/разности кубов двух выражений: 1) а3 - 1; 2) а3 - 8; 3) а6 - 1; 4) а3 - 0,027b3; 5) а6 - b12. 3. Верны ли равенства: 1) 4 - с2 = (4 - c)(4 + c); 2) 16x2 - m2 = (4x2 - m2)(4x2 + m2); 3) 27 - а3 = (9 + а)(9 + 6а + а2); 4) 125 + b3 = (5 + b)(5 + 5а + а2)?
Выполнение письменных упражнений 1. Разложите на множители: 1) х2 - 4; 2) 25 - 9а2; 3) 36m - 100n2; 4) 0,04р2 - 1,69q2; 5) х2у2 - 6) a4 - b6; 7) -1 + 49a4b8. 2. Разложите на множители по формуле разности квадратов: 1) (х - 1)2 - 49; 2) (3b - 5)2 - 49; 3) (2х - 3)2 - (х + 4)2; 4) а4 - (а - 7)2. 3*. Решите уравнение: 1) х2 - 64 = 0; 2) 4х2 - 25 = 0; 3) 9х2 + 16 = 0; 4) (2х - 3)2 - 36 = 0. 4. Разложите на множители: 1) m3 - n3; 2) с3 + 8; 3) 27а3 - b3; 4) 125 + a3b3; 5) х6 - у9; 6) 1000a12b3 + 0,001c9d15; 7*) (а + 7)3 - 8; 8*) (а - 12)3 + 27. 5*. Вычислите значение выражения
VI. Итоги урока Установите соответствие
Объясните выбор.
VII. Домашнее задание Повторить формулы сокращенного умножения. Используя формулы сокращенного умножения, выполнить такие задачи. № 1. Разложите на множители: 1) 36х2 - 169в2; 2) 0,09t4 - 121р2; 3) 1,69у14 - 900z8; 4) (4х - 3)2 - 25х2. № 2. (Разложите на множители). Представьте в виде произведения: 1) а3 + 64; 2) 0,008х3 - 0,027у3; 3) 4) 343а6b15 - 0,008х9у3. № 3. Опережающее домашнее задание. 1) Вместо □ подставьте в выражение такой одночлен, чтобы многочлен можно х2 + 2х + □; х2 - 6х + □; х2 + 12х + □; х2 - 5х + □. 2) Запишите данное выражение в виде квадрата двучлена. Каких значений, исходя из этого, может приобретать образован (а следовательно, и данное выражение? А если к нему прибавить положительное число а? 3) Представьте число в виде суммы двух положительных чисел, одно из которых (ближайшее к нему) точным квадратом: 3; 5; 10; 51; 38; 90.
|
|
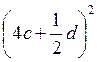 ; 2)
; 2) 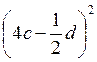 ;
; 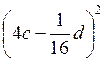 ; 4)
; 4) 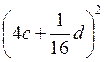 .
.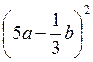 ; 2)
; 2) 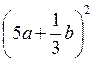 ;
; 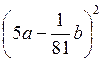 ; 4)
; 4) 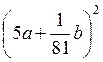 .
.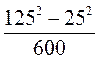 .
.