Урок № 48

Тема. Использование формул сокращенного умножения для разложения многочленов на множители

Цель: добиться осознания учащимися того факта, что изученные формулы сокращенного умножения применяются для разложения на множители многочленов определенного вида; начать работу по выработке умений выполнять разложение многочленов на множители с применением изученных формул (разложение многочленов на множители по формулам квадрата двучлена).

Тип урока: применение знаний, умений и навыков.

Ход урока

I. Организационный момент

Учащиеся проверяют свою готовность к уроку, учитель настраивает учащихся к уроку.

II. Проверка домашнего задания

@ Поскольку № 1 и 2 из домашнего задания являются упражнениями высокого уровня сложности, желательно тщательно проверить выполнение этих упражнений, прокомментировав каждый шаг преобразований (желательно использовать алгоритм работы с целым выражением, рассмотренный на предыдущем уроке).

III. Формулировка цели и задач урока

@Учитель, опираясь на опережающее домашнее задание (повторить формулы), напоминает учащимся, что на протяжении рассмотрения этой темы было изучено ряд формул сокращенного умножения, которые применялись для преобразования целых выражений в многочлен стандартного вида. А на этом уроке ученики будут учиться использовать те же самые формулы для обратного преобразования многочленов, а именно: для разложения на множители.

IV. Актуализация опорных знаний, умений, навыков

Работа с опережающим домашним заданием

Выполнение устных упражнений

1. Что называется разложением многочлена на множители?

2. Свойство умножения используется при разложении многочлена на множители вынесением общего множителя за скобки?

3. В какой последовательности выполняется разложение многочлена на множители способом группировки?

4. Какой многочлен тождественно равен выражениям (произведениям):

1) (a + b)2; 2) (a - b)(a + b);

3) (a - b)(a2 + ab + b2);

4) (a - b)2;

5) (a + b)(a2 - ab + b2)?

5. Произведение многочлена равна,

1) а2 + 2аb + b2; 2) а2 - b7; 3) а3 - b3; 4) а2 - 2аb + b2; 5) а3 + b3?

V. Применение знаний

@ После проведенной работы (см. выше) учителю остается обобщить полученные сведения и сформировать определенное представление учащихся, а именно:

Формулы сокращенного умножения применяются для:

1) преобразования целых выражений в многочлены стандартного вида;

2) преобразование многочленов в произведение - разложение многочленов на множители.

Для выполнения этого преобразования известные учащимся формулы лучше записать в новом виде (см. конспект 14).

VI. Усвоение умений

@ Поскольку на изучение этой темы отведено три урока, то желательно разбить учебный материал на блоки, которые последовательно изучать:

1-й блок: квадрат суммы и разности двух выражений;

2-й блок: разность квадратов; разность кубов;

3-й блок: использование всех формул.

На этом уроке традиционно начинаем обрабатывать достаточно сложные для разложения на множители квадрат суммы и квадрат разности, ибо надо сформировать у учащихся умение «видеть» квадраты одночлен, удвоенное произведение. С этой целью предлагаем ученикам сначала соответствующие устные упражнения, а потом уже переходить к выполнению письменных упражнений.

Выполнение устных упражнений

1. Представьте в виде квадрата выражения: 16; 9х2; 0,01х4у2.

2. Квадратом какого выражения является выражение: у4; х2у6; 0,25а2?

3. Подайте в виде удвоенного произведения несколькими способами:

16ху; х2а; 2х2у.

Выполнение письменных упражнений

1. Представьте трехчлен в виде квадрата двучлена:

1) х2 + 2ху + у2;

2) р2 - 2р + q + q2;

3) а2 + 12а + 36;

4) 64 + 16b + b2;

5) 1 - 2z+ z2;

6) n2 + 4n + 4.

2. Разложите на множители:

1) а2 + 8а + 16;

2) 9х2 - 6х + 1;

3) 121m2 - 88mn + 16n2;

4) 24аb + 36а2 + 4b2;

5) а6 - 4а3b + 4b2;

6) 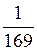х4 + 2х2у2 + 169у4.

3. Замените знак * одночленом так, чтобы образованный трехчлен можно было представить в виде квадрата двучлена:

1) * - 2by + y2;

2) 9с2 + 12с + *;

3) 64х2 - * + 81у2;

4) * + 30m3n2 + 9n4;

5) а4 - 0,8а6 + *;

6) * - аb + 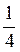b2.

4. Найдите значение выражения:

1) у2 - 2у + 1, если в = 101;

2) 4х2 - 20х + 25, если х = 12,5;

3) 25а2 + 49 + 70а, если а = 4,4;

4) 60b + 100b2 + 9, если b = 1,7.

5. Решите уравнение:

6. 1) х2 + 6х + 9 = 0;

7. 2) 25х2 - 30х + 9 = 0.

VII. Итог урока

Можно представить в виде квадрата двучлена выражение:

1) 4х2 + 12х + 9;

2) 25а2 - 30аb + 9b2;

3) р2 - 2р + 4;

4)100b2 + 9с2 - 60bс;

5) 49х2 + 12ху - 64у2;

6) 81у2 - 16z2 - 72уz?

Если можно, представьте в виде квадрата двучлена.

VIII. Домашнее задание

№ 1. Представьте трехчлен в виде квадрата двучлена:

1) а2 - 14а + 49;

2) 25у2 + 10y + 1;

3) 100а2 - 180аb + 81b2;

4) 16m2 + 49n2 - 112mn;

5) х10 - 6х5b + 9b2;

6) 36m6 + n12 + 12m3n6;

7) 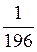х8 - 2х4у2 + 196у4;

8) 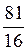а6 - 9а3b 2 + 4b4.

№ 2. Замените знак (*) одночлена так, чтобы образованный трехчлен можно было представить в виде квадрата двучлена:

1) (*) + 4аb + b2;

2) 25х2 - 10х + (*);

3) 49х2 - (*) + 4у2;

4) (*) - 25m5n + 36n2;

5) а4 - 0,6а5 + (*);

6) * - ху + 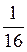у2.