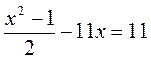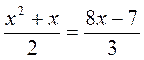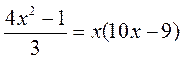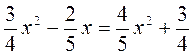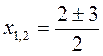|
III. Формулировка цели и задач урока Осознанному изучению вопроса урока (формула корней квадратного уравнения с четным вторым коэффициентом) будет способствовать поставленную учителем задачу: по изученным на предыдущем уроке формулами, выполняя устные вычисления, решить квадратное уравнение с достаточно большими коэффициентами (уравнение должно быть подобрано так чтобы дискриминантов был больше 10000, то есть не было возможности воспользоваться таблицей квадратов, приведенной в учебнике). Анализируя проблему, приходим к выводу о необходимости «совершенствования», изученных на предыдущем уроке формул. Изучение отдельных случаев применения формул корней квадратного уравнения и овладение умениями их использовать определяем как ведущую цель урока.
IV. Актуализация опорных знаний и умений @ Для успешного восприятия учащимися учебного материала урока следует активизировать такие знания и умения: выполнение тождественных преобразований иррациональных выражений; определение коэффициентов квадратного уравнения; определение дискриминанта квадратного уравнения и нахождения количества и значений корней квадратного уравнения по определенным значением дискриминанта. Выполнение устных упражнений 1. Укажите в квадратном уравнении его коэффициенты: а) 3у2 - 5у + 1 = 0; б) -х2 + х - 3 = 0; в) 12t - 7t2 + 4 = 0; г) 9t - 6 + t2 = 0; д) 5m - m2 = 0; есть) n2 - 7 = 0. 2. Упростите выражения: 3. Сколько корней имеет квадратное уравнение: x2 - 64 = 0; у2 + 49 = 0; 2р2 - 7р = 0; k2 = 0; 2х2 + 4х - 1 = 0; х2 + 3х + 4 = 0; у2 + 3у + 2
V. Применение знаний План изучения нового материала 1. Формулы корней квадратного уравнения для случая, если второй коэффициент уравнения парной. 2. Алгоритм применения новых формул. 3. Пример применения составленного алгоритма. @ В выводе «новых» формул корней квадратного уравнения для упрощения вида формул можно сразу ввести дополнительные обозначения:
VI. Формирование умений Выполнение устных упражнений 1. Среди данных квадратных уравнений выберите те, в которых четный второй коэффициент: a) 3в2 - 5у + 1 = 0; б) 12х - 7х2 + 4 = 0; в) х2 + 2х - 3 = 0; г) 10х2 + 3х - 7 = 0. 2. Найдите значение выражения а) b = -2; а = 3; с = -2; б) b = 6; а = 1; с = 2.
Выполнение письменных упражнений Для реализации дидактической цели урока следует решить задачи следующего содержания: 1. Решения квадратного уравнения по формулам. 1) Решите уравнение: а) х2 - 2х - 1 = 0; б) 7х2 - 18х + 8 = 0; в) 3х2 + 22х - 16 = 0; г) х2 + 21х + 90 = 0; д) 3х2 + 53х - 18 = 0; есть) -25х2 + 50х + 75 = 0; ж) х2 + 0,5 х - 1,5 = 0; с) 2х2 - х + ы) х2 - 2) Решите уравнение: б) 5х2 - 16х + 3 = 0; в) х2 + 2х - 80 = 0; г) х2 - 22х - 23 = 0; д) 4х2 - 36х + 77 = 0; есть) 15у2 - 22у - 37 = 0; ж) 7z2 - 20z + 14 = 0; с) у2 - 10у - 25 = 0. 2. Решение квадратного уравнения наиболее удобным способом. а) 2х2 - 5х - 3 = 0; б) 3х2 - 8х + 5 = 0; в) 5х2 + 9х + 4 = 0; г) 36у2 - 12y + 1 = 0; д) 3t2 - 3t + 1 = 0; есть) х2 + 9х - 22 = 0; ж) у2 - 12в + 32 = 0; с) 100х2 - 160х + 63 = 0. 3. Решение уравнений с предварительным выполнением равносильных преобразований и избранием наиболее удобного способа решения. 1) Решите уравнение: а) t2 + 3t = - 4t - 6 - t2; б) 5(y2 + 3) = -24у + 20; в) 4х(х - 2) + х2 = 6х + 3; г) 6х2 + 3х = 5(2х + 1); д) (х - 1)2 + 4х2 = 0; е) (3х - 2)(3х + 2) = 6х + 3; ж) 5х2 - с) 2) Найдите корни уравнения: а) 3(х + 4)2 = 10х + 32; б) 15х2 + 17 = 15(х + 1)2; в) (x + 1)2 = (2х - 1)2; г) (х- 2)2 + 48 = (2 - 3х)2. 3) Решите уравнение: а) 4) Решите уравнение: а) 0,7х2 = 1,3x + 2; б) 7 = 0,4в + 0,2у2; в) х2 - 1,6х - 0,36 = 0; г) z2 - 2z + 2,91 = 0; д) 0,2у2 - 10y + 125 = 0; есть) 4. Логические упражнения и задачи повышенного уровня сложности для учащихся, имеющих достаточный и высокий уровни знаний. Вставьте пропущенный выражение.
@ Письменные упражнения имеют целью закрепление новых формул корней квадратного уравнения (уравнения с четным вторым коэффициентом) и формирование умений применять эти формулы (новые знания) в сочетании с изученными ранее способами решения квадратных уравнений. На уроке продолжается усвоение формул корней квадратного уравнения, поэтому, как и на предыдущем уроке, с целью предупреждения ошибок и лучшего запоминания формул, следует требовать от учащихся соблюдения алгоритма (см. конспект) и устного и письменного воспроизведения выведенных формул. На этом уроке можно предложить учащимся задания, предусматривающего выполнение равносильных преобразований уравнений перед применением изученных формул, при этом следует выделить уравнения, в которых возникает необходимость преобразования уравнения с дробными коэффициентами в уравнение с целыми коэффициентами (умножением обеих частей уравнения на НСК знаменателей дробных коэффициентов) и на уравнения с целыми коэффициентами, имеют общий делитель, отличный от нуля. Также обращаем внимание учащихся на удобство овладение еще и таким приемом: старший коэффициент квадратного уравнения лучше иметь положительным (в идеале - равен единице).
VII. Итоги урока В каком случае правильно найдены корни? а) х2 - 2х - 8 = 0, D1 = 1 + 8 = 9, б) х2 + 2х - 8 = 0, D1 = 2 + 8 = 10, в) x2 - 4х - 12 = 0, D1 = 4 + 12 = 16, х1,2 = 2 ± 4, х1 = 6, х2 = -2.
VIII. Домашнее задание 1. Выучить все формулы корней квадратного уравнения. 2. Решить примеры на применение этих формул. 3. На повторение: тождественные преобразования рациональных выражений и выражений, содержащих квадратные корни.
|
| ||||||||||||||||||||||||||||||||||||||||||||
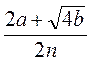 ; (2
; (2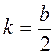 ,
, 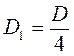 и во время решения опорных примеров уже начинать закрепление новых обозначений. Так же как и на предыдущем уроке, после вывода формул следует дать учащимся ориентировочную схему решения квадратного уравнения этим способом и в развязывании опорного задача требовать строгого ее соблюдения.
и во время решения опорных примеров уже начинать закрепление новых обозначений. Так же как и на предыдущем уроке, после вывода формул следует дать учащимся ориентировочную схему решения квадратного уравнения этим способом и в развязывании опорного задача требовать строгого ее соблюдения.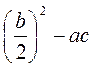 , если:
, если: