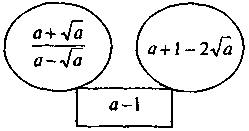|
III. Формулировка мсти и задач урока С целью создания соответствующей мотивации предлагаем учащимся решить ряд уравнений: несколько из них - неполные квадратные уравнения, а другие - квадратные уравнения общего вида, причем два из них такие, что полный квадрат выделяется легко (например, возведенные квадратные уравнения с четным вторым коэффициентом), а два такие, что выделение полного квадрата затруднено (квадратные уравнения, не являются сводными). Анализ сложившейся ситуации приводит к формулировке проблемы: необходимо найти единственный достаточно простой алгоритм решения квадратных уравнений общего вида. Решение этой проблемы и является главной целью урока.
IV. Актуализация опорных знаний и умений @ С целью успешного восприятия учащимися учебного материала перед его изучением следует активизировать знания и умения учащихся: приемы выделения квадрата двучлена из данного квадратного трехчлена; вычисление значений переменных по формулам; решение уравнений вида х2 = а. Выполнение устных упражнений 1. Решите уравнения: а) х2 = 25; б) 4х2 = 1; в) 3х2 = 6; г) (х - 1)2 = 25; д) (х + 2)2 = 0. 2. Замените уравнения равносильными приведенными квадратными уравнениями: а) 2х2 - 6х + 10 = 0; б) 3х2 - 12х2 + 3 = 0; в) 2х + 0,5х2 - 1 = 0; г) -х2 + х - 7 = 0. 3. Подайте трехчлен, если возможно, в виде квадрата двучлена:
V. Усвоение знаний План изучения нового материала 1. Вывод формулы корней квадратного уравнения. Схема решения квадратного уравнения общего вида по формуле. 2. Примеры применение выведенной формулы. @ Вывод формулы корней квадратного уравнения общего вида традиционно осуществляется в форме решения квадратного уравнения общего вида выделением квадрата двучлена. И хотя перед этим уроком была решена упражнения на повторения (возобновления навыков выделения квадрата двучлена), вывод формулы может вызвать определенные трудности, потому что связано с преобразованиями выражений с буквенными коэффициентами. Поэтому, чтобы преодолеть такие трудности, перед выводом формулы можно еще раз показать все преобразования на примере уравнения с числовыми коэффициентами, а затем переходить к работе с буквенными выражениями (или же в случае невысокого уровня математических способностей учащихся подать их в виде готовых формул). После вывода формулы важно дать учащимся схему действий с применение выведенных формул в виде алгоритма. Рассматривая примеры на применение выведенных формул, желательно обратиться к всех возможных случаев (дискриминантов положительный, отрицательный и равен нулю). При решении квадратного уравнения, дискриминантов которого равна нулю, следует показать два способа нахождения корней (двух равных): по выведенной формуле (которую в 9 классе будем изучать как формула абсциссы вершины параболы - графика квадратичной функции у = ах2 + bх + с), а также разложением левой части уравнения на множители по формуле квадрата двучлена (этот способ пригодится для построения графика квадратичной функции путем геометрических преобразований графика функции у = х2).
VI. Формирование умений Выполнение устных упражнений 1. Найдите значение выражения b2 - 4aс: а) а = 1; b = 2; с = 3; б) а = 2; b = 5; с = -3. 2. Найдите значение выражения 3. Сколько корней имеет уравнение ах2 + bx + c = 0, если значение выражения b2 - 4ас для него равна: а) 25; б) 3; в) -1; г) 0?
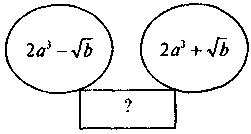
Выполнение письменных упражнений Для реализации дидактической цели урока следует решить задачи следующего содержания: 1. Нахождения дискриминанта квадратного уравнения и определение количества корней этого уравнения. 1) Для квадратного уравнения найдите дискриминантов и укажите число его корней: а) 2х2 - 3х + 1 = 0; б) 4х2 + 4х + 1 = 0; в) -3х2 + 6x - 4 = 0. 2) Вычислите дискриминантов квадратного уравнения и укажите число его корней: а) 2х2 + 3х + 1 = 0; б) 2х2 + х + 2 = 0; в) 9х2 + 6х + 1 = 0; г) х2 + 5х - 6 = 0. 2. Решение квадратного уравнения по формуле. 1) Решите уравнение: а) х2 - 6х + 5 = 0; б) х2 + 4х - 12 = 0; в) х2 + 7х + 10 = 0; г) х2 - 3х + 4 = 0; д) х2 - 10х + 25 = 0; есть) х2 - 4х - 21 = 0. 2) Решите уравнение: а) 2х2 - 5х + 3 = 0; б) 2х2 + х - 1 = 0; в) 3х2 + 5х - 2 = 0; г) 4х2 - 4х + 1 = 0; д) 2х2 - 3х + 2 = 0; есть) 7х2 - 6х - 1 = 0. 3) Решите уравнение: а) 3х2 - 7х + 4 = 0; б) 5х2 - 8х + 3 = 0; в) 3х2 - 13х + 14 = 0; г) 2у2 - 9y + 10 = 0; д) 5у2 - 6y + 1 = 0; есть) 4х2 + х - 33 = 0; ж) у2 - 10y - 24 = 0; с) р2 + р - 90 = 0. 3. Не решая квадратного уравнения, указать те из них, которые имеют заданное количество корней. 1) Не решая уравнения, укажите те из них, которые имеют один корень: а) 9х2 + 6х + 1 = 0; б) 3х2 - х - 4 = 0; в) 2х2 - 16х + 32 = 0. 2) Какое из уравнений не имеет корней: а) х2 + 2х - 7 = 0; б) 2х2 - 3х + 8 = 0; в) 3х2 + 5х + 4 = 0? 4. Решение квадратного уравнения наиболее удобным способом (задание предполагает повторение понятие неполного квадратного уравнения и способы его решения в сочетании с изученным на уроке способом решения квадратных уравнений общего вида). 5. Логические упражнения и задачи повышенного уровня сложности для учащихся, имеющих достаточный и высокий уровни знаний. 1) Найдите значения b, при которых один из корней уравнения равен -3: a) 20x2 + bx - b2 = 0; б) 2) Докажите, что при любом значении переменной значение выражения положительно: а) а2 + 4а + 11; б) 3) Вставьте пропущенный выражение:
@ Письменные упражнения имеют целью усвоение формул корней квадратного уравнения (формулы дискриминанта, корней) и формирование умения применять эти формулы (новые знания) в сочетании с изученными ранее способами решения квадратных уравнений (изученный ранее материал). Поскольку на этом уроке только начинается работа по закреплению знаний формул корней квадратного уравнения, с целью предупреждения ошибок и лучшего запоминания изученных формул, следует требовать от учащихся строгого соблюдения алгоритма и устного и письменного воспроизведения выведенных формул (целесообразно использовать такой мнемонический прием запоминания формул в виде предложения - «где равен бэ квадрат минус четыре а это», или использовать другие мнемонические приемы). Если усвоение нового материала проходит успешно, то уже на этом уроке можно предложить учащимся задания, что предполагает сочетание новых знаний и умений (формул корней квадратного уравнения и первичных умений их применять) с приобретенными ранее знаниями и умениями (виды квадратных уравнений и умение определять вид квадратного уравнения - сводное или неполное определенного вида, и способов решения неполных квадратных уравнений).
VII. Итоги урока В каком случае правильно найдено дискриминантов? а) 5х2 + 3х + 2 =0, D = 49; б) 2х2 - 3х - 5 = 0, D = 49; в) (3х - 2)(3х + 2) = 6х+3, D = 49; г) 2х2 - 3x + 5 = 0, D = 49.
VIII. Домашнее задание 1. Изучить формулы корней квадратного уравнения. 2. Решить примеры на применение этих формул. 3. На повторение: подобрать примеры заданий на преобразование выражений, содержащих квадратные корни, решение которых предусматривает вынесение множителя из-под знака корня, и задачи на сокращение дробей.
|
| ||||||||||||||||||||||||||||||||
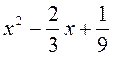 .
.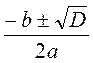
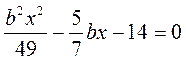
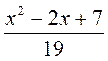 в)
в) 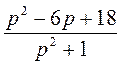 .
.