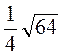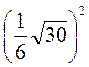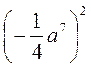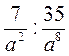УРОК № 49

Тема. Числовые последовательности. Свойства числовых последовательностей

Цель урока: добиться усвоения учащимися содержания понятий: числовая последовательность, n-й член числовой последовательности, формула п-го члена; список способов задания числовой последовательности. Выработать умения: воспроизводить изученные определения; находить члены последовательности с заданными номерами, если последовательности заданы различными способами. Повторить определение числовой функции, а также сопутствующие понятия.

Тип урока: усвоение знаний, выработка умений.

Наглядность и оборудование: опорный конспект № 28.

Ход урока

I. Организационный этап

Учитель проверяет готовность учащихся к уроку, настраивает их на работу.

II. Проверка домашнего задания

На уроке разбираются наиболее сложные вопросы контрольной работы, которые ученики не могли проработать дома.

III. Формулировка цели и задач урока.

Мотивация учебной деятельности учащихся

На этом этапе урока учителю следует привести как можно больше числовых последовательностей, с которыми учащиеся могут встречаться в повседневной жизни, а также при изучении основ наук. Таким образом подготавливают учащихся к восприятию мысли о том, что предметом изучения математики являются не только выражения, уравнения, неравенства и т.п.; математика изучает также результаты наблюдений за реальными физическими, химическими процессами, климатическими явлениями, которые выражаются в виде рядов чисел, каждое из которых стоит в этой записи на строго определенном месте. После этого вполне логично сформулировать задачи: изучить вопрос об эти «ряды чисел», а также возможности дальнейшего применения этих понятий на практике. Таким образом формулируется в общем виде основная дидактическая цель урока.

IV. Актуализация опорных знаний и умений учащихся

Устные упражнения

1. Найдите значение выражения:

1) -2,6 + 0,5;

2) -2,1 : (-0,01);

3) (0,45)4 : 0,418;

4) ;

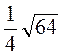5) ;

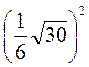6) ;

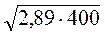7) (3 - 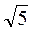)(3 + ).

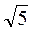2. Упростите выражение:
1) (4b + 1) - (3 - b);

2) ;

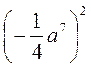3) (2x - 1)(х - 2);

4) а5 ∙ а12 : а16;

5) ;

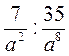6) 3x2y5 ∙ (-x3y2).

3. Найдите значение выражения:

1) х + 10у при х = 1,5, у = -;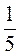

2) 2x2 + 1 при х = -4;

3) х2 + 6х - 2 при х = 3.

V. Формирование знаний

План изучения нового материала

1. Определение числовой последовательности. Понятие члена последовательности.

2. Виды числовых последовательностей:

1) в зависимости от количества ее членов;

2) в зависимости от тенденции ее членов (растущая, убывающая, такая, что не является возрастающей или убывающей).

3. Способы задания числовых последовательностей:

1) перечнем ее членов;

2) описанием ее членов;

3) таблицей;

4) формуле (n-го члена);

5) рекурентною формуле.

Опорный конспект № 28

Методический комментарий

Материал этого урока является вспомогательным для изучения материала последующих уроков, поэтому рассматривается лишь в объеме, необходимом для изучения арифметической и геометрической прогрессий. Ученики должны на примерах числовых последовательностей усвоить необходимую для дальнейшего изучения материала терминологию: последовательность, член последовательности", " номер члена последовательности, формула п-го члена последовательности, рекуррентная формула.

VI. Формирование умений

Устные упражнения

1. Дана последовательность: 0,1; 7; 0,2; 8; 0,3; 9. Укажите:

1) сколько членов имеет эта последовательность;

2) третий член последовательности;

3) какой номер имеет член последовательности, равный 0,3;

4) член последовательности является следующим за числом 8; предыдущим к числу 7.

2. Последовательность (хn) задана формулой хn = n + 5. Укажите первые три члена этой последовательности. Является ли эта последовательность возрастающей? бесконечной?

Письменные упражнения

Для реализации дидактической цели урока следует решить упражнения такого содержания:

1) для последовательности записать номер члена, предшествующего члена с заданным номером; является следующим за членом с заданным номером;

2) найти первые несколько членов последовательности, заданной: а) описанием; б) формулой n-го члена; в) рекурентно;

3) составить формулу п-го члена последовательности, заданной описанием или перечислением ее членов;

4) найти номер члена последовательности (является ли данное число членом последовательности), заданной формулой n-го члена.

Методический комментарий

Все упражнения, которые планируется решить на уроке, должны быть направлены на закрепление изученной терминологии, а также на выработку умений работать с формулой n-го члена числовой последовательности (которую можно использовать как прямо, для вычисления члена числовой последовательности с заданным номером, так и для решения обратной задачи для заданного числа, что является членом числовой последовательности, найти его номер). Также следует уделить внимание выработке умений учащихся работать с рекурентными формулами, специфика которых заключается в том, что для вычисления члена последовательности, что стоит на определенном месте, следует в формулу подставлять не его номер, а предыдущий (предыдущие члены). Во время выполнения всех упражнений на вычисление обращаем внимание на отработку вычислительных навыков учащихся.

VII. Итоги урока

Контрольные вопросы

1. Приведите примеры числовых последовательностей.

2. Приведите пример числовой последовательности: 1) конечно; 2) бесконечной.

3. Приведите пример последовательности, заданной формулой n-го члена. Назовите какой-нибудь член этой последовательности.

4. Приведите пример последовательности, заданной рекурентною формуле.

VIII. Домашнее задание

1. Изучить определения понятий, рассмотренных на уроке (см. опорный конспект № 28).

2. Решить упражнения, аналогичные по содержанию и уровню сложности выполненной на уроке.

3. Повторить преобразование рациональных выражений.