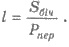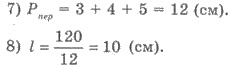ГЕОМЕТРИЯ

Раздел ІІ. СТЕРЕОМЕТРИЯ

§15. ПРИЗМА.

3. Площади полной и боковой поверхностей призмы.

Площадью полной поверхности призмы называют сумм площадей всех ее граней, а площадью боковой поверхности призмы - сумма площадей ее боковых граней.

Площадь S_полн полной поверхности призмы выражается через площадь S_бич ее боковой поверхности и площадь S_осн основ призмы формулой

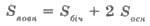
Теорема о площади боковой поверхности прямой призмы. Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы, то есть на длину бокового ребра.

Пример 1. В основе прямой призмы лежит равносторонняя трапеция, меньшее основание которой равно 3 см, боковая сторона 4 см, а угол при основании 60°. Найти площадь боковой поверхности призмы, если ее высота равна большем основании трапеции.

Решения. 1) Пусть АВСDА₁В_1sub>С1D₁ - четырехугольная призма, заданная в условии; DС = 3 см, АD = 4 см, DAB = 60° (рис. 454).

2) Выполним планиметрический рисунок трапеции АВСD, что лежит в основе призмы (рис. 455), и проведем в ней высоты DК и СL.

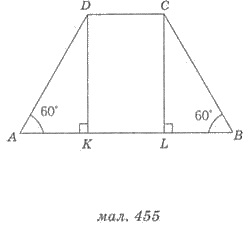
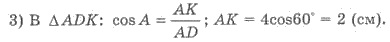
4) КDСL - прямоугольник, поэтому КL = DС = 3 см.

5) ∆ВАК = ∆СВL (по катетом и гипотенузой), поэтому АК = L; L = 2 см.

6) Тогда АВ = 2 + 3 + 2 = 7 (см).

7) Высота призмы ВР₁ по условием равна большем основании трапеции. Итак, ВВ₁ = 7 см.

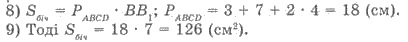
Пусть в наклонной призме проведено сечение, перпендикулярное боковым ребрам, пересекает все боковые ребра (сечение KLM на рисунке 456). Тогда боковую поверхность наклонной призмы можно найти по формуле:

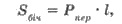
где P_пер - периметр сечения; l - длина бокового ребра.

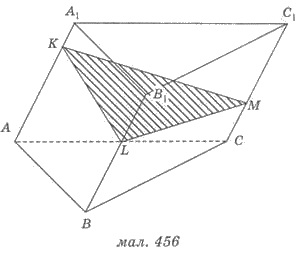
Пример 2. В наклонной треугольной призме две боковые грани взаимно перпендикулярні. их общее боковое ребро находится на расстояниях 3 см и 4 см от двух других боковых ребер. Найти длину бокового ребра призмы, если площадь ее боковой поверхности равна 120 см².

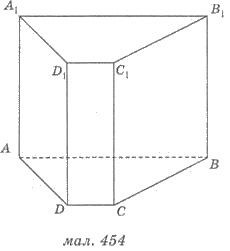
Решения. 1) Пусть АВСА₁В₁С₁ - наклонная призма, у которой КL - расстояние между параллельными ребрами ВВ₁ и АА₁, боковые грани АВВ₁А₁ и ВВ₁С₁С взаимно перпендикулярны (рис. 456).

2) Выберем на ребре ВВ₁ некоторую точку L и проведем КL ВВ₁ и LМ ВВ₁; LМ - расстояние между параллельными ребрами ВВ₁ и СС₁, по условию КL = 3 см; LМ = 4 см.

3) Поскольку КL ВВ₁ и LМ ВВ₁, то КLМ ВВ₁ (по признаку перпендикулярности прямой и плоскости). Поэтому КLМ - угол между боковыми гранями АВВ₁А₁ и ВВ₁С₁С. По условию КLМ=90°.

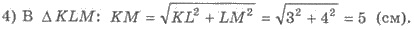
5) Сечение КLМ перпендикулярное боковым ребрам призмы.

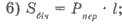тоди боковое ребро