ГЕОМЕТРИЯ

Раздел ІІ. СТЕРЕОМЕТРИЯ

§15. ПРИЗМА.

2. Сечения призмы.

Рассмотрим некоторые простейшие сечения призмы.

Сечение призмы, который проходит через два боковых ребра, не принадлежащих одной основе, называют диагональным сечением.

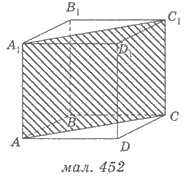
На рисунке 452 АА₁С₁С - диагональный сечение прямой призмы. Это сечение является прямоугольником, одна из его сторон - диагональ основания АС, а другая - боковое ребро АА₁. В наклонной призме диагональным сечением является параллелограмм.

Часто в задачах необходимо не только построить сечение, но и найти его площадь или периметр, или использовать сечение с другой целью.

Пример 1. В основе прямой призмы лежит ромб со стороной 4 см и острым углом 60°. Найти площадь диагонального сечения призмы, одной из сторон которого является большая диагональ ромба, если боковое ребро призмы равна 2 см.

Решения. 1) Пусть ABCDA₁B₁C₁D₁ - призма, в основании которой лежит ромб ABCD, АВ = 8 см, A = 60°, АС - большая диагональ ромба (рис. 452). Тогда АСС₁А₁ - диагональный сечение, площадь которого необходимо найти. CC₁ = 2 см (по условию).

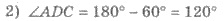
3) В ∆ADC по теореме косинусов: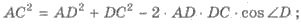

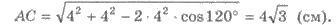
4) Тогда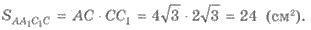

Часто в задачах рассматривают сечения призмы, проходящих через сторону основания призмы и которые пересекают боковые ребра призмы.

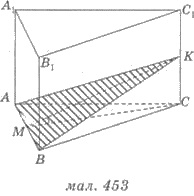
Пример 2. В основе прямой призмы лежит равносторонний треугольник, сторона которого равна 2 см. Через сторону этого треугольника проведено сечение, которое образует угол 30° с плоскостью основания и пересекает боковое ребро в его середине. Найти длину бокового ребра призмы.

Решения. 1) Пусть АВСА₁В₁С₁ - треугольная призма, основание которой - равнобедренный треугольник АВС, АВ = 2 см (рис. 453).

2) Через сторону АВ основу треугольника проведено сечение АВК, где К - середина СС₁.

3) Проведем в треугольнике АВС медиану СМ, которая также является высотой этого треугольника: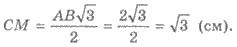

4) Поскольку CM AB и CM является проекцией КМ на плоскость АВС, то по теореме о трех перпендикуляры: КМ АВ.

Тогда КМС - угол, который образует сечение с плоскостью основания. По условию КМС = 30°.

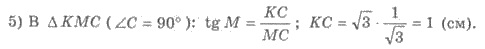
6) Так как К - середина СС₁, то СС₁ = 2КС = 1 ∙ 2 = 2 (см).