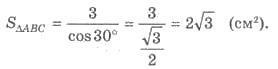ГЕОМЕТРИЯ

Раздел ІІ. СТЕРЕОМЕТРИЯ

§12. УГЛЫ В ПРОСТРАНСТВЕ.

4. Ортогональное проектирование.

Отдельным случаем параллельного проектирование является ортогональное проектирование.

Параллельное проектирование, направление которого перпендикулярен к плоскости проекции, называют ортогональным проектированием. Параллельную проекцию фигуры, образующейся при ортогональном проектировании, называют ортогональной проекцией фигуры.

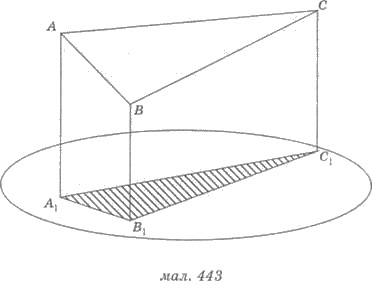
На рисунке 443 треугольник A₁B₁С₁ является ортогональной проекцией треугольника ABC.

Важной является следующая теорема.

Теорема о площади ортогональной проекции. Площадь ортогональной проекции многоугольника на плоскость равна произведению его площади на косинус угла между плоскостью многоугольника и плоскостью проекции.

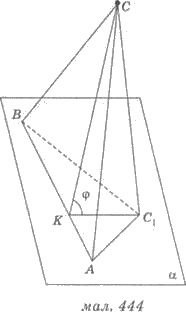
Пусть ∆АВС ортогонально проектируется на плоскость α, проходящая через сторону АВ этого треугольника (рис. 444). Имеем ∆АВС₁ - ортогональную проекцию ∆АВС, СС₁ α. Проведем С₁К АВ, тогда по теореме о трех перпендикуляры, получим СК АВ. Поэтому CKC₁ = φ - угол между плоскостью ∆АВС и плоскостью α. Из рассмотренной теоремы получим

Пример. Ортогональной проекцией треугольника АВС на плоскость α является прямоугольный треугольник А₁В₁С₁ с катетами 2 см и 3 см (рис. 443). Найти площадь треугольника АВС, если угол между плоскостями АВС и А₁В₁С₁ равен 30°.

Решения.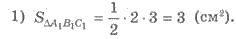

2) Поскольку - угол между плоскостями АВС и А₁В₁С₁, то