ГЕОМЕТРИЯ

Раздел ІІ. СТЕРЕОМЕТРИЯ

§12. УГЛЫ В ПРОСТРАНСТВЕ.

2. Угол между прямой и плоскостью.

Если прямая параллельна плоскости или ей принадлежит, то считают, что угол между прямой и плоскостью равен 0°. Если прямая перпендикулярна к плоскости, то угол между ними, естественно, считаем равным 90°.

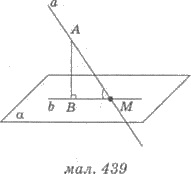
Пусть даны прямая а, пересекающая плоскость а в точке М и не является перпендикулярной к этой плоскости (рис. 439). Основы перпендикуляров, опущенных из точек прямой а на плоскость αb принадлежат прямой b (рис. 439). Эту прямую b называют проекцией прямой а на плоскость α.

Углом между плоскостью и прямой, пересекает плоскость и не является перпендикулярной к плоскости, называют угол между прямой и ее проекцией на плоскость.

На рисунке 439 угол АМВ является углом между прямой а и плоскостью а. Очевидно, что угол φ между прямой и плоскостью удовлетворяет условие 0° ≤ φ ≤ 90°.

Аналогично угла между прямой и плоскостью определяется угол между наклонной и плоскостью.

Пример. Из точки к плоскости проведена наклонная длиной 12 см. Найти угол, который образует наклонная с плоскостью, если проекция наклонной равна 6 см.

Решения. 1) На рисунке 439 наклонная АМ = 12 см, проекция наклонной на плоскость ВМ = 6 см. Необходимо найти величину угла АМВ.