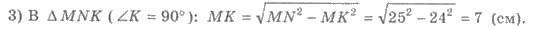ГЕОМЕТРИЯ

Раздел ІІ. СТЕРЕОМЕТРИЯ

§11. РАССТОЯНИЯ В ПРОСТРАНСТВЕ.

5. Расстояние между плоскостями.

Если плоскости пересекаются, то естественно считать, что расстояние между такими плоскостями равен нулю.

Расстоянием между параллельными плоскостями называют длину перпендикуляра, проведенного из любой точки одной плоскости до другой.

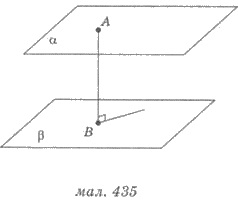
На рисунке 435: α || β, А α, АВ β, β. Длина отрезка АВ - расстояние между параллельными плоскостями α и β.

Пример. Концы отрезка МN длиной 25 см относятся параллельным плоскость α и β. Проекция отрезка на одну из плоскостей равна 24 см. Найти расстояние между плоскостями α и β.

Решения. 1) МК - перпендикуляр, опущенный из точки М на плоскость β, МК - искомое расстояние, (рис. 436).

2) Тогда NК - проекция МN на плоскость β. По условию NК = 24 см.