ГЕОМЕТРИЯ

Раздел ІІ. СТЕРЕОМЕТРИЯ

§11. РАССТОЯНИЯ В ПРОСТРАНСТВЕ.

4. Расстояние между прямыми, принадлежащими одной плоскости.

Если прямые пересекаются, то естественно считать, что расстояние между ними равно нулю.

Расстоянием между параллельными прямыми называют длину перпендикуляра, проведенного из любой точки одной из прямых до другой.

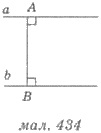
На рисунке 434: а || b, А 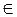α,. Длина отрезка АВ - расстояние между параллельными прямыми а и Ь.

Пример. АВСDА₁В₁С₁D₁ - куб, ребро которого равно 4 см. Найти расстояние между прямыми АD и В₁С₁.

Решение (рис. 433). 1) Поскольку АD || ВС и В₁С₁ || ВС, то АD || В₁С₁.

2) СD является проекцией прямой С₁D на плоскость АDС. Поскольку СD АD, то по теореме о трех перпендикуляры С₁D АD.

3) Поэтому длина отрезка С₁D - расстояние между прямыми АD и В₁С₁.