ГЕОМЕТРИЯ

Раздел ІІ. СТЕРЕОМЕТРИЯ

§11. РАССТОЯНИЯ В ПРОСТРАНСТВЕ.

3. Расстояние от прямой до плоскости.

Если прямая принадлежит плоскости или пересекает плоскость, то естественно считать, что расстояние от прямой до плоскости равна нулю.

Расстоянием от прямой до параллельной ей плоскости называют длину перпендикуляра, проведенного из любой точки прямой к плоскости.

На рисунке 432: а || α, А 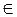а, АВ α. Длина отрезка АВ - расстояние от прямой а в плоскости α.

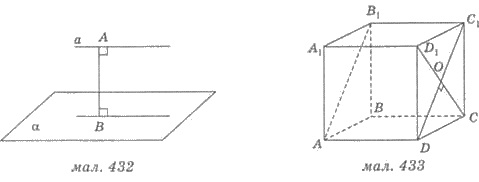
Пример. АВСDА₁В₁С₁D₁ - куб (рис. 433), ребро которого равно 2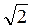 см.

Найти расстояние от прямой ВС до плоскости АВ₁С₁.

Решения. 1) Так как ВС || В₁С₁, то прямая ВС параллельна плоскости АВ₁С₁.

2) СD₁ С₁D, точка О - точка пересечения диагоналей боковой грани СD₁ и С₁D.

3) СО АВ₁С₁; СО - искомое расстояние.