Урок № 48
Тема. Метод геометрических мест
Цель: добиться усвоения
учениками схемы действий, которые положены в основу метода геометрических мест.
Сформировать умения:
·
воспроизводить
схему, что лежит в основе метода геометрических мест;
·
выполнять
действия, предусмотренные этой схемой.
Тип урока: усвоение знаний,
умений и навыков.
Наглядность и
оборудование: набор
демонстрационного чертежных принадлежностей.
ХОД УРОКА
I. Организационный
момент
II. Проверка
домашнего задания
Выполнение устных
упражнений проверяем во время фронтальной беседы, письменных упражнений - по образцу.
III. Мотивация
учебной деятельности. Формулировка цели и задач урока
Для мотивации
предлагаем учащимся выполнить задание:
1) найдите ГМТ,
равноудаленных от точек A и B;
2) найдите ГМТ,
удаленных от точек A и B на определенное расстояние a;
3) найдите ГМТ,
равноудаленных от точек A, B, C (точки A, B, C не лежат на одной прямой).
Сравнение условий
предложенных задач приводит к формулировке проблемы, которую надо
решить: как построить геометрическое место точек, удовлетворяющих одновременно
две (а не одну) условия?
Поиск ответа на
этот вопрос и является основной дидактической целью урока.
IV. Усвоение новых
знаний
Рассуждения, что
лежат в основе метода геометрических мест являются достаточно простыми и понятными
учащимся. Изложение этих соображений учитель может проводить индуктивным или
дедуктивным методом, то есть на примере одной из предложенных на третьем
этапе задач продемонстрировать ход рассуждений, а затем обобщить эти рассуждения
или наоборот-сформулировав общие утверждения, затем рассмотреть примеры его
применение.
VI. Первичное
осознание нового материала
Выполнение
письменных упражнений
В условиях следующих
задач устно выделить два условия, которые должны удовлетворять искомое ГМТ.
1. Точки A, B, C не
лежат на одной прямой. Постройте точку, равноудаленную от точек A, B, C.
Ответ. Искомая точка,
во-первых, равноудаленная от точек A и B, во-вторых, равноудалена от точек B и
C.
2. Даны точки A, B, C.
Постройте точку, которая равноудалена от точек A и B и лежит на заданной
расстояния от точки C.
3.
Постройте
точку, равноудаленную от сторон данного угла, которая лежит на расстоянии d от его
вершины.
4. Точка A лежит на
круге радиуса R. Постройте точки данного круга, удаленные от точки A на расстояние R.
После выполнения
такого анализа условий задач, начинаем письменное решение задач № 1 и № 3.
VII. Итоги урока
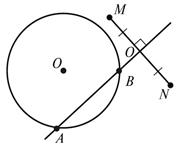
По рисунку сформулируйте
задачу, решением которой являются точки A и B.
VIII. Домашнее
задача
Решить задачи №
2, 4 классной работы.
Решить методом
геометрических мест задачу.
Задача. Найдите
геометрическое место центров окружностей радиуса R, проходящих через данную точку A.
Источники:
1. Уроки геометрии. 7 класс./ С. П. Бабенко
- Х.: Изд. группа «Основа», 2007.- 208 с.