Урок № 47
Тема. Геометрическое место точек
Цель:
·
сформировать
у учеников представление о содержании понятия «геометрическое место точек», свойство и
признак точек, принадлежащих ГМТ ;
·
сформировать
знание содержания и схемы доказательства теоремы о ГМТ.
Сформировать умения:
·
воспроизводить
определение свойства и признаки ГМТ, теорем о ГМТ;
·
использовать
эти утверждения при решении несложных задач на построение искомого ГМТ.
Тип урока: усвоение знаний,
умений и навыков.
Наглядность и
оборудование: набор
демонстрационного чертежных принадлежностей.
ХОД УРОКА
I. Организационный
момент
II. Проверка
домашнего задания
Само - или взаємоперевірка
за образцом.
III. Мотивация
учебной деятельности. Формулировка цели и задач урока
Учитель предлагает
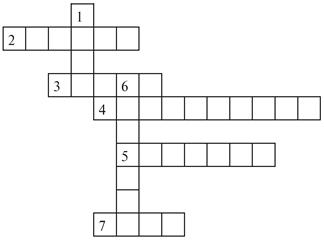
ученикам разгадать кроссворд.
1.
Все
точки плоскости, равноотстоящих от данной точки плоскости.
2. Отрезок,
соединяющий вершину треугольника с основанием перпендикуляра, проведенного из этой вершины
к стороны.
3. Отрезок,
соединяет две точки окружности и не проходящей через его центр.
4. Все точки плоскости,
что равноудалены от сторон угла.
5. Отрезок,
соединяющий вершину треугольника с серединой противоположной стороны.
6. Хорда, проходящая
через центр круга.
7. Все точки плоскости,
находящихся от данной точки на расстоянии, не большей за данную.
После
«разгадывание» учитель проводит беседу, смысл которой заключается в том, что учитель
побуждает учащихся к сравнению определений данных фигур с описаниями, данными в
«загадках». В ходе этого сравнения формулируется вывод: описание фигуры может
иметь вид определения (конструктивного) или описания, что характеризует общую
свойство всех точек фигуры.
Поскольку с новым
видом описания фигур учащиеся имеют дело впервые, следует более подробно изучить такой
способ описания фигуры-это и будет целью урока.
VI. Актуализация
опорных знаний
Выполнение
устных упражнений
1. На рисунке 1 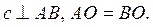 Докажите, что AC =
BC.
Докажите, что AC =
BC.
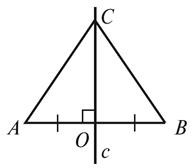
2.
На
рисунке 1 AC = BC. Докажите, что 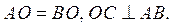
3.
На рисунке
2 AD - биссектриса угла BAC. Докажите, что BD = DC.
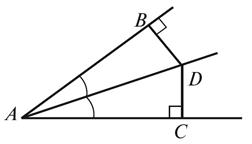
4. На рисунке 2 BD = DC.
Докажите, что AD - биссектриса угла BAC.
V. Усвоение новых
знаний
План изучения
нового материала
1°. Определение ГМТ.
Примеры ГМТ.
2°. Свойство точек
ГМТ и признак ГМТ точек.
3°. Основные теоремы о
ГМТ:
а) теорема о
срединный перпендикуляр;
б) теорема о
бісектрису угла.
Методический комментарий
В отличие от
учебника О. В. Погорелова, новый учебник содержит:
а) подробное толкование
ГМТ, сформулированы два взаємообернені утверждение, доведение которых позволяет
сделать вывод, что данная фигура является ГМТ;
б) сформулированную и
доказанную теорему о бісектрису угла.
Поскольку схема
доказательство обеих теорем о ГМТ одинакова, то работу по изучению их доказывания можно
организовать так: теорему о серединный перпендикуляр доказывает учитель,
теорема о бісектрису угла выносится на самостоятельное проработки в малых группах
с последующей презентацией доказывания.
VI. Первичное
осознание нового материала
Выполнение
устных упражнений
1. Фигура F -
геометрическое место точек, удовлетворяющих условие P. верно Ли, что:
а) на плоскости
существуют точки, которые удовлетворяют условию P, но не принадлежат F;
б) среди точек
фигуры F есть точки, не удовлетворяющие условия P;
в) любая точка,
что удовлетворяет условию P, принадлежит фигуре F?
2. Можно круг
радиуса 5 см считать геометрическим местом точек, удаленных от центра этого
круга на расстояние:
а) длиной 5 см;
б) не больше 5 см;
в) не менее 5 см;
г) не больше 4 см?
3.
Отрезок
AB равна 4 см. Можно ли считать срединный перпендикуляр до этого отрезка
геометрическим местом точек, которые:
а) отдаленные от A и
B на 2 см;
б) отдаленные от A и
B на одинаковые расстояния;
в) являются вершинами
рівнобедреник треугольников с основанием AB?
4. Луч BD - биссектриса
угла ABC. Можно ли считать его геометрическим местом точек, которые равноудалены:
а) от лучей BA и
BC;
б) от прямых BA и BC?
Выполнение
письменных упражнений
1. Начертите
треугольник ABC.
а) Постройте
геометрическое место точек, равноудаленных от вершин A и B.
б) Постройте
геометрическое место точек, равноудаленных от сторон AC и AB.
в) Отметьте точку
пересечения построенных геометрических мест и опишите ее свойства.
2. Докажите, что
геометрическим местом точек, удаленных от данной прямой a на расстояние d, есть две
прямые, параллельные a и удаленные от нее на d.
VII. Итоги урока
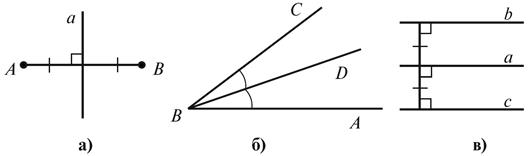
По рисунку 3 а, б,
в закончите предложения:
а) Прямая a -
геометрическое место точек, равноудаленных от...
б) Луч BD -
геометрическое место точек, равноудаленных от...
в) Прямая a -
геометрическое место точек, равноудаленных от...:
VIII. Домашнее
задача
Контрольные
вопрос
1. Дайте определение
геометрического места точек. Назовите геометрическое место точек, удаленных от
данной точки на заданное расстояние.
2. Сформулируйте и
докажите теорему о серединный перпендикуляр до отрезка.
3. Сформулируйте и
докажите теорему о бісектрису угла.
Решить задачи.
1. Начертите круг с
центром O и проведите хорду AB, которая является диаметром.
а) Постройте
геометрическое место точек, равноудаленных от точек A и B.
Проходит
построена прямая через точку O? Почему?
б) Постройте
геометрическое место точек круга, равноудаленных от сторон
угла AOB.
2. Геометрическим местом
точек, равноудаленных от двух параллельных прямых, является прямая, которая параллельна
данным прямым и проходит через середину их общего перпендикуляра.
Докажите.
3. Постройте
равнобедренный треугольник по основанию и углу, противоположным основе.
Источники:
1. Уроки геометрии. 7 класс./ С. П. Бабенко
- Х.: Изд. группа «Основа», 2007.- 208 с.