Урок № 48
Тема. Площадь трапеции
Цель: закрепить знание учащимися формул для вычисления площади треугольника. Рассмотреть формулу для вычисления площади трапеции. Формировать у учащихся умения и навыки применять эту формулу для вычисления площади трапеции.
Тип урока: усвоение умений и навыков.
Наглядность и оборудование: конспект «Площадь треугольника. Площадь трапеции».
Ход урока
I. Организационный этап
II. Проверка домашнего задания
Как и на нескольких предыдущих уроках, чтобы сэкономить время, на этом этапе урока ученики комментируют решение домашних задач с готовыми рисунками, выполненными на доске заранее (или самим учителем или учениками).
Усвоение содержания теоретического материала и его понимание проверяется во время самостоятельного выполнения учащимися тестовых заданий (см. Тетрадь для итогового и тематического оценивания).
Тестовое задание
Вариант И
1. Назовите формулу площади прямоугольника со сторонами а и b .
а) 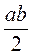 ; б)
; б) 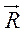 ; в) а2 + b2; г) ab.
; в) а2 + b2; г) ab.
2. Найдите площадь ромба ABCD, если АС = 5 см, BD = 8 см.
а) 20 см2; б) 40 см2; в) 10 см2; г) 13 см2.
3. По данным рисунка найдите площадь треугольника ABC.
а) 42; б) 84; в) 13; г) 21.
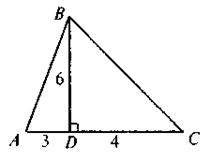
4. Найдите площадь прямоугольника со стороной 5 м и диагональю 13 м.
а) 60 см2; б) 60 м2; в) 65 м2; г) 156 м2.
5. Две стороны треугольника равны 8 см и 12 см, а высота, проведенная к меньшей из них, - 3 см. Найдите высоту, проведенную к большей стороне.
а) 4 см; б) 2 см; в) 4.5 см; г) 10 см.
6. Найдите площадь ромба со стороной 12 см и острым углом 30°.
а) 144 см2; б) 36см2; в) 72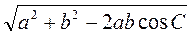 см2; г) 72 см2.
см2; г) 72 см2.
Вариант 2
1. Назовите формулу площади квадрата со стороной а.
а) 2а2; б) 4; в) а2; г) 4а2.
2. В паралелограмі ABCD до стороны AD проведена высоту ВК. Найдите площадь параллелограмма, если ВС = 8 см, ВК = 5 см.
а) 20 см2; б) 40 см2; в) 80 см2; г) 13 см2.
3. По данным рисунка найдите площадь три угольника ABC.
а) 30; б) 60; в) 15; г) 11.
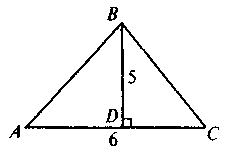
4. Найдите площадь прямоугольного треугольника с катетом 15 м и гипотенузой 17 м.
а) 127,5 м2; б) 60 м2; в) 120 м2; г) 60 см2.
5. Стороны параллелограмма равны 12 см и 16 см, а меньшая высота - 3 см. Найдите большую высоту параллелограмма.
а) 4 см; б) 2,25 см; в) 6 см; г) 14 см.
6. Найдите площадь параллелограмма со сторонами 8 м и 12 м и острым углом 30°.
а) 48 м2; б) 96 м2; в) 24 м2; г) другой ответ.
После окончания работы - проверка и коррекция.
III. Формулировка цели и задач урока
В зависимости от уровня интеллектуальной активности учащихся учитель или сам сообщает цель урока - изучение формулы для вычисления площади трапеции, или же предлагает учащимся выполнить практическое задание (на развитие конструктивного мышления).
Задача
1) Однажды Петя Пяточкин составил трапецию из четырех прямоугольных треугольников. Сможете ли вы повторить его достижение? «улучшить» (то есть сложить трапецию с меньшего количества прямоугольных треугольников)? Что общего имеют все треугольники в каждом из изображенных случаев?
2) Какой из случаев возможен для любой трапеции?
Решая задачи, учащиеся могут прийти к конфигураций, изображенных на рис. 1.
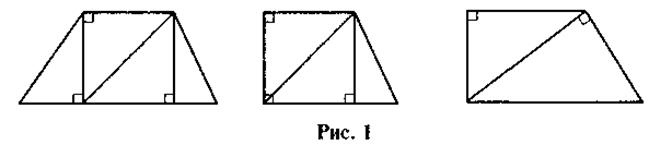
Решения задачи, кроме сугубо развивающего значения, помогает ученикам понять прием, который используют авторы учебника во время обоснования формулы площади трапеции - разбиение трапеции на треугольники с равными высотами, которые равны высоте трапеции, и со сторонами, являются основаниями трапеции. От понимания этого факта к формулировке цели урока один логичный шаг - если применить свойства площадей и формулу площади треугольника, то наверное можно вывести формулу для вычисления площади трапеции. Реализация этого плана (с последующим закреплением выведенной формулы и формированием умений применять формулу площади трапеции) - основная цель урока.
IV. Актуализация опорных знаний и умений
С целью успешного усвоения учащимися содержания теоремы, выражающей формулу площади трапеции, и идеи ее доведения, а также понимание учащимися возможности записи теоремы в виде S = MN h, ученикам следует активизировать знания и умения по аксиом площадей, формулы площади треугольника, определение трапеции, средней линии трапеции и ее свойства.
1. ABCD - трапеция (BC || AD), AD = a, BC = b, AM = BM, CN = ND. Какой из изображенных на рисунке 2 отрезков имеет длину:
а) 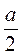 ; б)
; б) 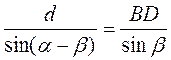 ; в)
; в) 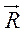 ; г)
; г) 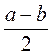 ?
?
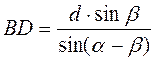
2. На медиане BD треугольника ABC (рис. 3) взято произвольную точку М. Докажите, что площади треугольников АВМ и СВМ равны.
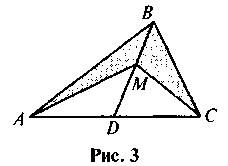
V. Усвоение знаний
План изучения нового материала
1. Теорема (формула площади трапеции).
2. Второе формулировка формулы площади трапеции.
VI. Формирование первичных умений
Выполнение устных упражнений
1. Две равновеликие трапеции имеют равные высоты. Означает ли это, что основы данных трапеций также соответственно равны?
2. Может ли диагональ трапеции делить ее на две равновеликие треугольники? Ответ обоснуйте.
3. Дано: ABCD - трапеция (BC || AD). Найдите 5, если:
а) ВС = 2 см; AD = 10 см; h = 5 см;
б) BC + AD = 16 см; h = 6 см;
в) средняя линия равна 10 см; высота 5 см;
г) r = 5 см; AB + CD = 18.
Выполнение письменных упражнений
1. Найдите площадь трапеции, если:
а) ее основания равны 4 см и 10 см, а высота - 6 см;
б) высота трапеции и ее средняя линия равна 8 см.
2. Основы рівнобедреної трапеции равны 8 см и 16 см, а острый угол - 45°. Найдите площадь трапеции.
3. Найдите площадь:
а) рівнобедреної трапеции с основами 15 см и 39 см, диагональ которого перпендикулярна боковой стороне;
б) прямоугольной трапеции с боковыми сторонами 12 см и 13 см, диагональ которой является биссектрисой острого угла.
VII. Итоги урока
Какая из фигур на рис. 4 лишняя? Почему?
VIII. Домашнее задание
Изучить формулу для вычисления площади трапеции.
Решить задачи.
1. Основания прямоугольной трапеции равны 6 см и 10 см, а большая боковая сторона - 5 см. Найдите площадь трапеции.
2. Найдите площадь рівнобедреної трапеции с основаниями 14 см и 50 см и диагональю 40 см.
3. В прямоугольной трапеции сумма оснований равна 20 см, а сумма боковых сторон - 30 см. Найдите площадь трапеции, если один из ее углов равен 30°.
4. Основы трапеции, вписанной в окружность, равны 12 см и 4 см. Найдите площадь трапеции, если в нее можно вписать круг.