Урок № 47
Тема. Площадь треугольника
Цель: добиться усвоения учащимися содержания и идеи доказательства теоремы о формуле плоти треугольника и следствий из нее. Сформировать умения:
· воспроизводить содержание изученных формул;
· записывать формулы согласно заданных обозначений элементов треугольников;
· применять изученные формулы к решению задач.
Тип урока, усвоения умений и навыков.
Наглядность и оборудование: конспект «Площадь треугольника. Площадь трапеции».
Ход урока
I. Организационный этап
II. Проверка домашнего задания
Учитель собирает тетради учеников с выполненной домашней самостоятельной работой (см. выше). Ученикам объявляется правильное решение за рисунками, изображенными на доске заранее.
III. Формулировка цели и задач урока
Для создания ситуации, что поможет учащимся понять идею доказательства теоремы о площади треугольника, предлагаем ученикам задачу.
Задача. На доске изображены две фигуры: параллелограмм ABCD и треугольник MNK такие, что AD = МК, и высоты проведенные к этим сторонам (ВН, NF), также равны (см. рис).
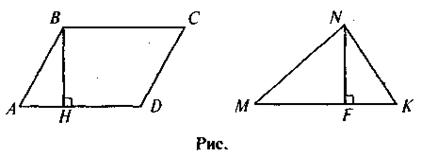
Площадь параллелограмма известна. Как найти площадь треугольника?
Поиск ответа на вопрос задачи помогает учащимся осознать:
· во-первых, существование противоречия между приобретенными знаниями и содержанием задачи (ученики умеют находить площади прямоугольника и параллелограмма, а по смыслу задачи следует найти площадь треугольника);
· во-вторых, содержание задачи содержит «подсказку» - вычисление площади треугольника следует как-то связать с вычислением площади параллелограмма.
Итак, цель урока - преодоление противоречия, то есть изучение формулы для вычисления плоти треугольника; средством выведения искомой формулы является формула площади параллелограмма.
IV. Актуализация опорных знаний
С целью успешного усвоения учащимися содержания и доказательства теоремы о формуле площади треугольника, а также следствий из нее, ученикам следует активизировать знания и умения по свойству диагонали параллелограмма и диагоналей ромба, свойства площадей равных фигур, аксиом площадей, определение прямоугольного треугольника, определение равностороннего треугольника и формулы вычисления высоты равностороннего треугольника через его сторону.
1. Какая из фигур на рис. 1 лишняя? Почему?
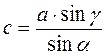
2. Прямые а и b параллельны. Площадь параллелограмма ABCD равна S. Чему равны площади других фигур на рис. 2 (AD = МК = SR)?
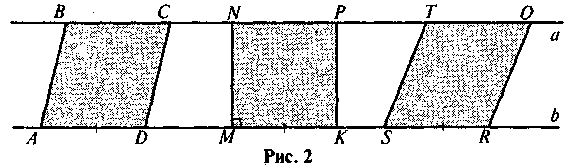
3. В треугольнике ABC АВ = ВС = а ,  А = 60°. Чему равна ВН и АР (ВН
А = 60°. Чему равна ВН и АР (ВН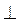 АС, АР
АС, АР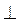 ВС)? Найдите длины этих отрезков, если АВ = 3 см, PC = 2 см, AC = 4
ВС)? Найдите длины этих отрезков, если АВ = 3 см, PC = 2 см, AC = 4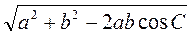 см (рис. 3).
см (рис. 3).
4. В паралелограмі ABCD AB = 7, BD = 6, PA0B = 18 (рис. 4). Найдите AC.
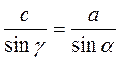
5. Найдите углы ромба ABCD , если известно, что:
a)  ABD = 53° ; б)
ABD = 53° ; б)  CDE = 32°; в) ВК
CDE = 32°; в) ВК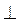 AD,
AD,  KBD = 20°.
KBD = 20°.
V. Усвоение знаний
План изучения нового материала
1. Теорема (формула площади треугольника).
2. Площадь прямоугольного треугольника.
3. Площадь ромба.
4. Площадь равностороннего треугольника.
5. Свойство медианы треугольника.
@ Изложения формулировка и доказательство теоремы, выражающей формулу вычисления площади треугольника, является классическим. Поэтому изучение этой части материала урока можно провести традиционно: учащимся предлагается самостоятельно рассмотреть соответствующий пункт учебника и изучить содержание и составить план доказательства теоремы. После выполнения этой работы непонятные моменты доведение комментируются учителем, содержание закрепляется на таком задании.
По рис. 5 дополнить записи, чтобы они стали верными равенствами.
S - площадь ΔMNK;
S = ... MK · NR;
S = 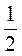 MN · ...
MN · ...
S = ...MF ...
... = MN · SK.
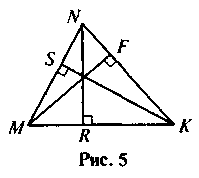
Изучение следствий из доказанной формулы для площади треугольника можно провести, поощряя учащихся к исследованиям вопросами:
· Существует ли треугольник, сторона которого является высотой? Как записать доказанную формулу для площади такого треугольника?
· Существует ли треугольник, все высоты которого равны? Как выражается высота этого треугольника через его сторону? Как записать формулу площади для такого треугольника?
· На какие фигуры ромб разбивается всеми своими диагоналями? Что вы знаете про эти фигуры? Как выражается площадь ромба через площадь этих треугольников?
Закончив обсуждение вопросов, ученики выполняют соответствующие записи в тетрадях. (Чтобы ученики осознали логические связи между изученными на уроке формулами, записи этих формул можно записать в виде схемы, рис. 6.)
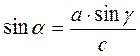
Конспект 19 |
Площадь треугольника. Площадь трапеции
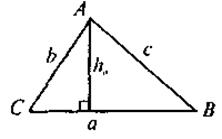
Если в ΔABC: ha - высота, проведенная к стороне a, то SАВС = 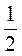 aha. aha.
Последствия |
|
1) Если в ΔABC  С = 90°, то С = 90°, то |
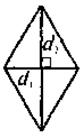
2) Если d1 и d2 диагонали ромба, то |
3) Если треугольник равносторонний со стороной a, то |
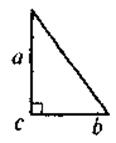
|
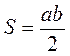
|
|
|
|
|
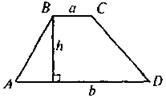
Если в трапеции ABCD (BC || AD) BC = a, AD = b,
h - высота, то 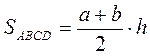 или S = MN · h ( MN - средняя линия) или S = MN · h ( MN - средняя линия) |
|
|
|
|
|
|
|
|
|
VI. Формирование первичных умений
Выполнение устных упражнений
1. Площадь треугольника ABC равна S. Чему равна площадь параллелограмма ABCD, три вершины которого совпадают с вершинами данного треугольника?
2. По какой формуле целесообразно вычислять площадь прямоугольного треугольника, если известны:
а) длины гипотенузы и проведенной к ней высоты;
б) длины двух катетов?
3. Два равновеликие треугольники имеют равные высоты. Означает ли это, что основы данных треугольников также равны?
4. Докажите, что большей стороне треугольника всегда соответствует меньшая высота.
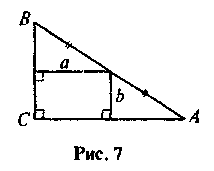
5. Какова площадь треугольника ABC на рис. 7?
6. В паралелограмі провели диагонали. Равны ли площади всех образованных четырех треугольников?
Выполнение письменных упражнений
1. По данным рисунка 8 найдите площадь треугольника ABC.
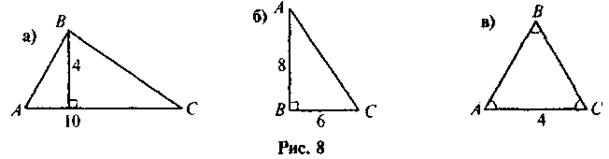
2. Найдите площадь:
а) равнобедренного треугольника с основанием 10 см и боковой стороной 13 см;
б) треугольника ABC, в котором АВ = 17 см, а высота ВН делит сторону АС на отрезки АН = 8 см и НС = 2 см.
3. Площадь треугольника равна 72 см2. Найдите периметр треугольника, если его высоты равны 9 см, 12 см и 24 см.
4. Найдите площадь ромба, диагонали которого равны 8 м и 20 м.
5. Найдите площадь:
а) треугольника ABC с высотой ВН , если АВ= 13 см, ВС = 15 см, ВН = 12 см, а точка Н лежит на отрезке АС;
б) прямоугольного треугольника, гипотенуза которого делится высотой на отрезки длиной 9 см и 4 см;
в) равностороннего треугольника с высотой 2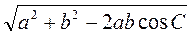 см.
см.
6. На рисунке 9 представлен единичный квадрат. Найдите площадь заштрихованной фигуры.
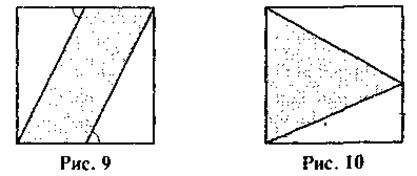
7. На рисунке 10 представлен единичный квадрат. Найдите площадь заштрихованной фигуры.
VII. Итоги урока
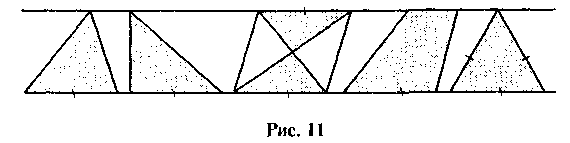
Какая из фигур на рисунке 11 лишняя? Почему?
VIIИ. Домашнее задание
Изучить содержание теоремы, ее доказательство и последствия.
Решить задачи.
1. Найдите площадь:
а) прямоугольного треугольника с гипотенузой 20 см и катетом 12 см;
б) остроугольного треугольника ABC с высотой AN = 4 см, если ВН = 2 см.  C = 45°.
C = 45°.
2. Найдите гипотенузу прямоугольного треугольника, если его площадь равна 20 см2. а высота, проведенная из вершины прямого угла, - 4 см.
3. Найдите диагонали ромба, если одна из них вдвое больше другой, а площадь ромба равна 64 см2.
4. Найдите площадь равнобедренного треугольника с периметром 16 см и высотой длиной 4 см. проведенной к основанию.
5. Начертите остроугольный треугольник и проведите в нем высоты. Проведите необходимые измерения и вычислите:
а) площадь данного треугольника;
б) площади треугольников, на которые данный треугольник делится высотой.

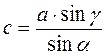

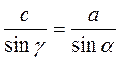
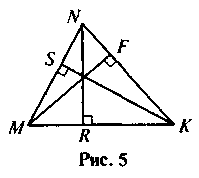
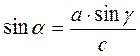

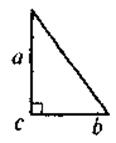
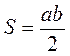


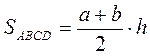 или
или 



