Урок 48

Тема. Понятие о движении, равенство фигур в пространстве

Цель урока: формирование понятий: движение, равные фигуры. Доведение новой свойства движения: плоскость во время движения переходит в плоскость.

Оборудование: схемы «Расстояние между двумя точками» (см. урок 46) и «Координаты середины отрезка» (см. урок 48), модель куба.

Ход урока

И. Проверка домашнего задания

1. Ответить на вопросы учащихся, возникшие в процессе решения задач № 16, 18.

2. Математический диктант.

Куб ABCDKLMN расположен в системе координат:

вариант 1 - рис. 264; вариант 2 - рис. 256, диагональ грани куба равна 2.

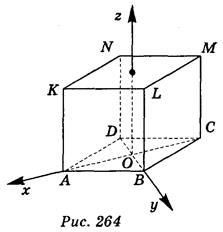
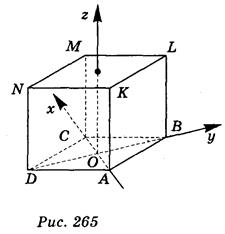
Запишите координаты точки, которая симметрична:

1) точке А относительно точки О; (2 балла)

2) точке L относительно оси z; (2 балла)

3) точке N относительно плоскости ху; (2 балла)

4) точке К относительно плоскости вz; (2 балла)

5) точке М относительно точки О; (2 балла)

6) точке В относительно точки К. (2 балла)

Ответ. Вариант 1. 1) C(-1; 0; 0); 2) N(0; -1; ); 3) (0;-1;-);4) М(-1;0;); 5) (1;0;-); 6) (2;0;2).

Вариант 2. 1) C(1;0;0); 2) N (0; -1; ); 3) (0;-1;-); 4) M(1;0;); 5) (-1;0;-); 6) (-2;0;2).

II. Восприятие и осознание нового материала

Движение в пространстве

Движением в пространстве называется преобразование, при котором сохраняются расстояния между точками. Докажем общие свойства движений.

Теорема 1.

Точки, лежащие на прямой, при движении переходят в точки, лежащие на прямой, и сохраняется порядок их взаимного расположения.

Доведение

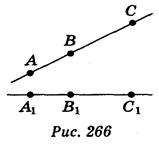
Пусть точки А, В, С лежат на прямой, причем точка В - между точками А и С, то есть АВ + ВС = АС (рис. 266). Если движение отражает данные точки на точки А1, В1, С1, то А1В1 = АВ, А1C1 = АС , В1С1 = ВС , т.е. имеет место равенство А1B1 + В1С1 = А1С1. А это означает, что точка1 лежит между точками А1 и С1. Теорема доказана.

Следствие. Движение отражает прямую в прямую, луч - в луч, отрезок - в отрезок, равный данному.

Теорема 2.

Движение отражает треугольник на треугольник, равный данному.

Доведение

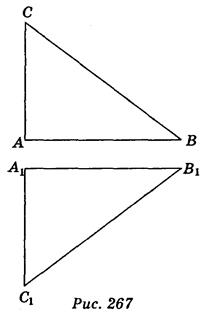
Пусть дан произвольный треугольник АВС (рис. 267). Движение отражает его стороны АВ, ВС, АС на отрезки А1B1, В1С1, А1С1, причем A1B1 = АВ, В1С1 = ВС, А1С1 = АС, следовательно, ΔА1В1С1 = ΔАВС. Теорема доказана.

Следующая теорема характеризует новое свойство движения в пространстве.

Теорема 3.

Движение отображает плоскость на плоскость.

Доведение

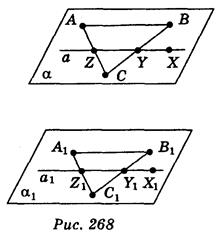
Пусть α - произвольная плоскость (рис. 268), возьмем на ней любые точки А, В, С не лежат на одной прямой. Во время движения точки А, В, С перейдут в точки А1, B1, C1, которые не лежат на одной прямой. Проведем через точки А1, B1, C1 плоскость α1. Докажем, что во время движения α переходит в плоскость α1. Пусть X - произвольная точка α. Проведем через нее в плоскости α прямую а, которая пересекает треугольник АВС в двух точках Z и Y. Прямая а перейдет в некоторую прямую а1. Точки Y, Z прямой а перейдут в точки Z1, Y1, которые принадлежат треугольник А1В1С1, а потому и плоскости α1. Итак, прямая а1 лежит в плоскости α1. Точка Х во время движения переходит в точку X1 прямой a1, а потому и плоскости α1. Теорема доказана.

Две фигуры называются равными, если они совмещаются движением.

Решение задач

1. Приведите примеры движений.

2. Даны два равных отрезка с общим концом. Какими движениями один из них можно отобразить на второй?

3. Задача № 20* из учебника (с. 55).

4. Приведите примеры равных фигур из окружения.

5. Дано два уровня кубы с общей гранью. Какими движениями их можно совместить?

6. Задача № 21 из учебника (с. 55).

III. Домашнее задание

§4, п. 28; контрольные вопросы № 6-8; задача № 19 (с. 55).

IV. Подведение итога урока Вопросы к классу

1) Какое преобразование фигуры называется движением?

2) В какую фигуру во время движения переходит плоскость?

3) Какие фигуры в пространстве называются равными?