Урок 47
Тема. Преобразование симметрии в пространстве. Симметрия в природе и на практике
Цель урока: формирование знаний учащихся о преобразование симметрии в пространстве и применение знаний к решению задач.
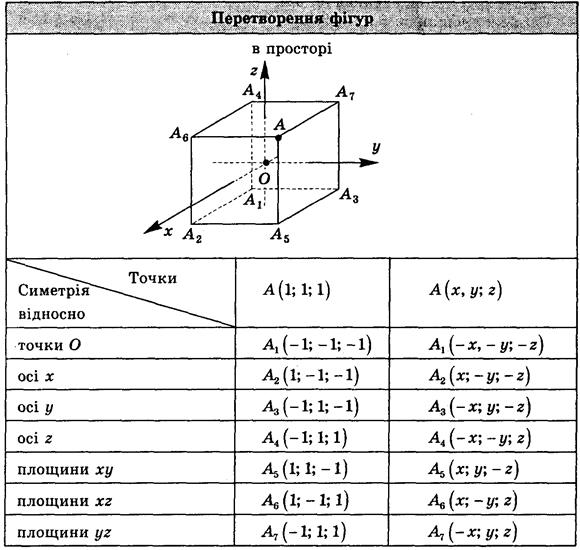
Оборудование: схема "Преобразование фигур».
Ход урока
И. Проверка домашнего задания
1. Устное комментирование решения домашних заданий.
2. Математический диктант.
Дан треугольник АВС:
вариант 1 - А (2; 0; 2), В (2; 2; 0), С (0; -2; 2);
вариант 2 - А (2; 0; 0), В (2; - 2; 2), С (0; - 2; 0).
Точки K, L, M - середины сторон АВ, AC, BC (рис. 256).
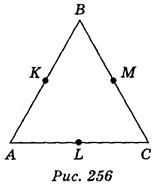
Пользуясь изображением, запишите:
1) координаты точки К; (2 балла)
2) координаты точки L; (2 балла)
3) координаты точки М; (2 балла)
4) длину средней линии KL; (2 балла)
5) длину медианы AM; (2 балла)
6) координаты точки D, если четырехугольник ABCD - параллелограмм. (2 балла)
Ответ. Вариант 1. 1) К(2; 1; 1); 2) L (1; -1; 2); 3) M(1; 0; 1); 4) KL = 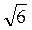 ; 5) AM =
; 5) AM =  ; 6) D(0; -4; 4).
; 6) D(0; -4; 4).
Вариант 2. 1) К (2; - 1; 1) ; 2) L(1; -1; 0); 3) M(1; -2; 1); 4) KL = ; 5) АМ =
; 5) АМ = 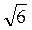 ; 6) D(0; 0; -2).
; 6) D(0; 0; -2).
II. Восприятие и осознание нового материала
Понятие симметрии относительно точки в пространстве
Определение симметрии относительно точки, известно из планиметрии, остается правильным и для стереометрии.
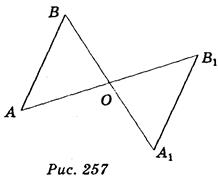
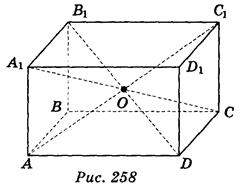
Точки А и А, называются симметричными относительно точки О, если точка О - середина отрезка AA1. Преобразование, при котором каждая точка данной фигуры отображается на точку, симметричную ей относительно точки О, называется симметрией относительно точки О, или центральной симметрией. На рис. 257 отрезок АВ при симметрии относительно точки А переходит в отрезок A1B1. Если симметрия относительно некоторой точки О отражает данную фигуру на ту же фигуру, такую фигуру называют центрально-симметричной, а точка О - ее центром симметрии. Например, центрально-симметричной фигурой является прямоугольный параллелепипед, точка пересечения его диагоналей - центр симметрии (рис. 258).
Решение задач
1. Дано точки А (и; 2; 3). Найдите координаты точки А1, симметричной точке А относительно начала координат. (Ответ. А1(-1;-2;-3))
2. Точки А (5; -3; 4) и В(-3; 1; - 2) симметричны относительно точки С. Найдите координаты точки С. (Ответ. С(1; -1; 1))
3. Точка А (1; 2; 3) симметрична точке В относительно точки С(3; 2; 1). Найдите координаты точки В. (Ответ. В (5; 2; -1))
4. Симметричны любые две точки пространства относительно некоторой третьей точки?
5. Сколько центров симметрии имеет:
а) отрезок;
б) прямая;
в) круг;
г) плоскость;
д) куб?
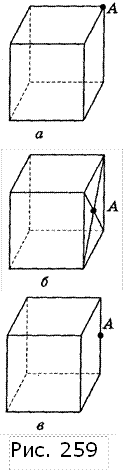
6. Дан куб. Постройте от руки фигуру, симметричную кубу относительно точки А (рис. 259).
Понятие симметрии относительно прямой в пространстве
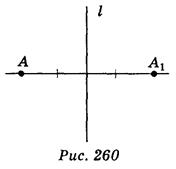
Точки А и А1 называются симметричными относительно прямой l, если прямая l проходит через середину отрезка АА1 и перпендикулярна к нему (рис. 260).
Преобразование, которое отображает каждую точку фигуры на точку, симметричную ей относительно данной прямой, называется симметрией относительно прямой (или осевой симметрией).
Решение задач
1. Даны точки А (1; 2; 3). Найдите координаты точки, симметричной ей относительно оси: а) х; б) в; в) z.
(Ответ. Аx(1;-2;-3); y(-1; 2;-3); Аz(-1; -2; 3).)
2. Что такое ось симметрии?
3. Сколько осей симметрии имеет:
а) отрезок;
б) прямая;
в) круг;
г) плоскость;
д) куб.
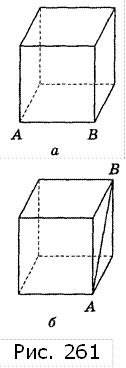
4. Дан куб. Постройте от руки фигуру, симметричную кубу относительно прямой АВ (рис. 261).
Понятие симметрии относительно плоскости
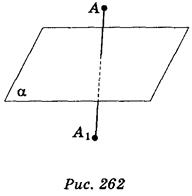
Точки А и A1 называются симметричными относительно плоскости α, если эта плоскость перпендикулярна к отрезка АА1 и делит его пополам (рис. 262). Преобразование, при котором каждая точка данной фигуры отображается на точку, симметричную ей относительно плоскости α, называется симметрией относительно плоскости α. Если преобразование симметрии относительно плоскости а переводит фигуру в себя, то фигура называется симметричной относительно плоскости α, а плоскость α называется плоскостью симметрии.
Решение задач
1. Задача № 17 из учебника (с. 55).
2. Сколько плоскостей симметрии имеет:
а) отрезок;
б) прямая;
в) круг;
г) плоскость;
д) куб?
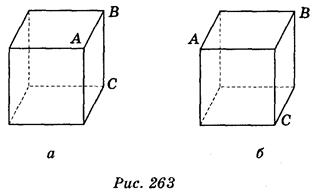
3. Дан куб. Постройте от руки фигуру, симметричную кубу относительно плоскости АВС (рис. 263).
III. Домашнее задание
§4, п. 26, 27; контрольные вопросы № 4, 5; задачи № 16, 18 (с. 55).
IV. Подведение итога урока
Подведение итога урока можно провести с использованием представленной ниже схемы.
Вопрос к классу
1) Что такое преобразование симметрии относительно точки?
2) Что такое преобразование симметрии относительно прямой?
3) Что такое преобразование симметрии относительно плоскости?