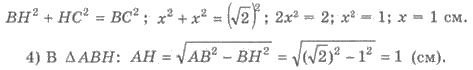ГЕОМЕТРИЯ
Раздел ІІ. СТЕРЕОМЕТРИЯ
§8. ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ. ПРОЕКЦИЯ НАКЛОННОЙ НА ПЛОСКОСТЬ.
2. Свойства перпендикуляра и наклонной.
Рассмотрим свойства
перпендикуляра и наклонной.
1) Перпендикуляр, опущенный из данной
точки к плоскости, меньше любой наклонной, проведенной из этой же точки
к плоскости.
На рисунке 411: АН АК.
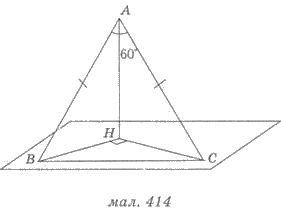
2) Если две наклонные, проведенные из
данной точки к плоскости, равны, то равны их проекции.
На рисунке 412 из точки А к плоскости
а проведены две наклонные АК и АK1 и перпендикуляр АН и АК = АК1. Тогда по свойству: НК = НК1.
3) Если две наклонные, проведенные из
данной точки к данной плоскости, имеют равные проекции, то они равны между собой.
На рисунке 412 из точки А к плоскости
а проведены две наклонные АК и АK1 и перпендикуляр АН, причем КН = К1Н. Тогда по свойству: АК = АК1.
4) Если из данной точки проведены к
плоскости две наклонные, то большая наклонная имеет большую проекцию.
На рисунке 413 из точки А к плоскости
а проведены две наклонные АК и АL и перпендикуляр АН, AК > AL. Тогда по свойству: HК
> HL.
5) Если из данной точки проведены к
плоскости две наклонные, то большей из них является та, которая имеет большую проекцию на данную
плоскость.
На рисунке 413 из точки А к плоскости
а проведены две наклонные АК и АL и перпендикуляр АН, НК >
НL. Тогда по свойству: АК >
АL.
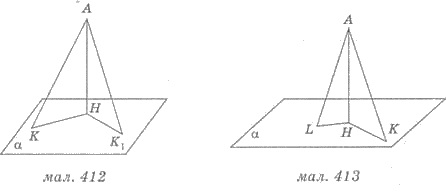
Пример 1. Из точки к плоскости
проведены две наклонные, длины которых 41 см и 50 см. Найти проекции наклонных, если
они относятся, как 3 : 10, и расстояние от точки до плоскости.
Решения. 1) АL = 41 см; АК = 50 см (рис. 413). По
свойством имеем НL НК. Обозначим НL = 3х см, НК = 10х
см, АН = h см. АН - расстояние от точки А до
плоскости α.
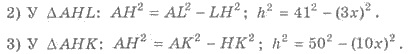
4) Приравнивая, получаем 412
- 9х2 = 502 - 100х2;
х2 = 9; х = 3 (учитывая х
> 0). Итак, НL
= 3 ∙ 3 = 9 (см), НК = 10 ∙ 3 = 30 (см).
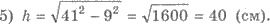
Пример 2. С данной
точки к
плоскости проведены две
наклонные, каждая по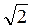 
см. Угол между наклонными равен 60°, а угол
между их проекциями - прямой. Найти расстояние от точки до плоскости.
Решения.
1) АС = ВС = 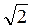см - наклонные, 
ВАС
= 60°; ВНС = 90° (рис. 414). Необходимо найти АН.
2) В рівнобедреному треугольнике АВС: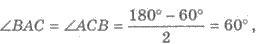 
поэтому ∆АВС - равносторонний; ВС = 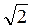см.
3) Так как АВ = АС, то НВ = НС; обозначим НВ = НС = х см. Тогда в ∆ВНС:
