УРОК № 47
Тема. Умножение вектора на число
Цель урока: формирование умения умножать вектор на число; изучение свойств умножения вектора на число; формирование умений применять изученные значение и свойства к решению задач.
Тип урока: комбинированный.
Наглядность и оборудование: таблица «Декартовы координаты и векторы на плоскости»[13].
Требования к уровню подготовки учащихся: описывают умножения вектора на число; откладывают вектор, равный произведению вектора на число; формулируют свойства умножения вектора на число; применяют изученные определения и свойства к решению задач.
Ход урока
И. Проверка домашнего задания
- 1. Проверить наличие выполненного домашнего задания и ответить на вопросы, которые возникли у учащихся при его выполнении.
- 2. Фронтальная беседа
- 1) Дайте определение суммы двух векторов. Опишите способы построения вектора суммы двух векторов.
- 2) Дайте определение разности двух векторов. Опишите способы построения вектора разности двух векторов.
- 3) Сформулируйте законы сложения и вычитания двух векторов.
II. Поэтапное восприятие и осознание нового материала
Умножение вектора на число
Произведением вектора  на действительное число λ называетесь вектор
на действительное число λ называетесь вектор  = λ
= λ , колінеарний вектора
, колінеарний вектора  , причем:
, причем:
- 1)
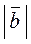 = |λ| ·
= |λ| · 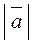 ;
;
- 2) если λ > 0, то вектор
 , одинаково направленный с вектором
, одинаково направленный с вектором  ;
;
- 3) если λ 0, то вектор
 противоположно направленный вектору
противоположно направленный вектору  (рис. 209).
(рис. 209).
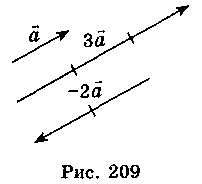
Свойства произведения вектора на число
- 1) (λ1λ2)
 = λ1(λ2
= λ1(λ2 ) (связующий закон);
) (связующий закон);
- 2) λ1
 + λ2
+ λ2 = (λ1 + λ2)
= (λ1 + λ2) (распределительный закон);
(распределительный закон);
- 3) λ
 + λ
+ λ = λ(
= λ( +
+  ) (распределительный закон);
) (распределительный закон);
- 4) 0 ·
 = λ ·
= λ · 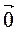 =
= 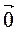 .
.
Два ненулевые векторы  и
и  коллинеарны тогда и только тогда, когда
коллинеарны тогда и только тогда, когда  = λ
= λ , λ - отличное от нуля число.
, λ - отличное от нуля число.
Координаты вектора λ равны произведению числа λ на соответствующие координаты вектора
равны произведению числа λ на соответствующие координаты вектора  . Если векторы заданы на плоскости, то λ
. Если векторы заданы на плоскости, то λ (а1; а2) = =
(а1; а2) = =  (λа1; λа2).
(λа1; λа2).
Решение упражнений
- 1. Постройте вектор
 , длина которого равна 4 см. Построй то с помощью линейки векторы:
, длина которого равна 4 см. Построй то с помощью линейки векторы:
а) 2 ; б) -2
; б) -2 ; в)
; в) 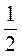
 ; г) -
; г) -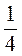
 .
.
- 2. Дано
 (1; -3),
(1; -3),  (-2; 1). Найдите координаты вектора:
(-2; 1). Найдите координаты вектора:
а) 2 ; б) -3
; б) -3 ; в) 2
; в) 2 + 3
+ 3 ; г) 2
; г) 2 - 3
- 3 .
.
- 3. Найдите |2
 |, если
|, если  (1; 2).
(1; 2).
- 4. Докажите, что векторы
 (1; 2) и
(1; 2) и  (0,5; 1) одинаково направлены, а векторы
(0,5; 1) одинаково направлены, а векторы 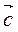 (-1; 2) и
(-1; 2) и 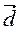 (0,5; -1) противоположно направлены.
(0,5; -1) противоположно направлены.
- 5. Абсолютная величина вектора λ
 равна 5. Найдите λ, если:
равна 5. Найдите λ, если:
а)  (-6; 8); б)
(-6; 8); б)  (3; -4).
(3; -4).
- 6. В паралелограмі ABCD О - точка пересечения диагоналей, К - середина стороны CD. Выразите векторы
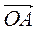 и
и 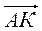 через векторы
через векторы 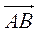 и
и 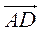 .
.
III. Закрепление и осмысление нового материала
Решение задач
- 1. В треугольнике ABC AM - медиана. Докажите, что
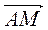 =
= 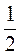 (
(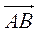 +
+ 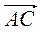 ).
).
- 2. Точки М и N - середины отрезков АВ и CD соответственно (рис. 210). Докажите, что
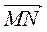 =
= 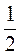 (
(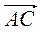 +
+ 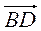 ).
).
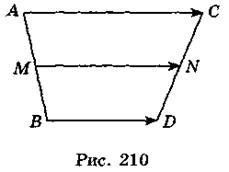
- 3. Дан параллелограмм ABCD,
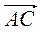 =
=  ,
, 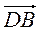 =
=  . Выразите векторы
. Выразите векторы 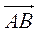 ,
, 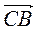 ,
, 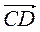 и
и 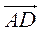 через
через  и
и  .
.
IV. Домашнее задание
- 1. Изучить теоретический материал.
- 2. Решить задачи.
- 1) Даны векторы
 (3; 2) и
(3; 2) и  (0; -1). Найдите вектор
(0; -1). Найдите вектор 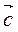 = -2
= -2 + 4
+ 4 и его абсолютную величину.
и его абсолютную величину.
- 2) В паралелограмі ABCD О - точка пересечения диагоналей, М - середина ВС. Выразите
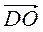 и
и 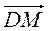 через векторы
через векторы 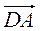 и
и 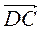 .
.
V. Подведение итогов урока
Вопрос к классу
- 1. Дайте определение умножения вектора на число.
- 2. Сформулируйте свойства произведения вектора на число.