Урок 46
Тема. Координаты середины отрезка
Цель урока: вывод формул для нахождения координат середины отрезка и применение этих формул к решению задач.
Оборудование: схема «Координаты середины отрезка».
Ход урока
И. Проверка домашнего задания
1. Ответить на вопросы, которые возникли у учащихся при выполнении задач № 4, 6, 7.
2. Самостоятельная работа.
Вариант 1
1) Найдите расстояние между точками А(-1; 0; 2) и В(1; -2; 3). (5 баллов)
2) Найдите на оси х точки, которые удалены от точки А (4; - 2; 3) на расстояние 7. (7 баллов)
Вариант 2
1) Найдите расстояние между точками А (2; 3; 1) и В(1; 1; -1). (5 баллов)
2) Найдите на оси точки, которые удалены от точки А(-3; 2; 4) на расстояние 13. (7 баллов)
Вариант 3
1) Найдите расстояние между точками А(-1; - 2; 3) и В(-2; 0; 1). (5 баллов)
2) Найдите на оси х точки, которые удалены от точки А(3; -4; 6) на расстояние 13. (7 баллов)
Вариант 4
1) Найдите расстояние между точками А (-2; -3; 1) и В(-1; - 1; 3). (5 баллов)
2) Найдите на оси z точки, которые удалены от точки А (-2; 3; 4) на расстояние 7. (7 баллов)
Ответ. Вариант 1. 1) 3; 2) (10; 0; 0) и (-2; 0; 0).
Вариант 2. 1) 3; 2) (0; 14; 0) и (0;-10;0).
Вариант 3. 1) 3; 2) (0; 0; 18) и (0;0;-6).
Вариант 4. 1) 3; 2) (0;0;-2) и (0; 0; 10).
II. Восприятие и осознание нового материала
Решение задач
Найдите координату середины отрезка АВ, если:
а) А(5) и(9); б) А(-3) и В(7); в)А(а) и В(b).
Найдите координаты середины отрезка АВ, если:
а) А(3;2) и B(1; 4); б) A(xA ; yA) и В(хB ; B).
Формулы для координат середины отрезка, если заданы координаты его концов.
Утверждение.
Каждая координата середины отрезка равна полусумме соответствующих координат его концов.
Доведение
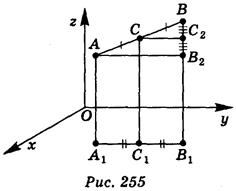
Пусть А (хA; A; zA) и В(хB; B; zB) - две произвольные точки пространства. Выразим координаты середины С отрезка АВ через координаты его концов А и В (рис. 255). Через точки А, В, С проведем прямые, параллельные оси z, которые пересекут плоскость ху в точках А1(хА, уА, 0), B1 (хB, уB, 0), С1(xC, C, 0) соответственно. Известно, что в координатной плоскости координаты середины отрезка выражаются через координаты его концов по формулам: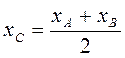 
; 
.
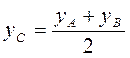Проведя АА2 || А1B1 и СС2 || А1В1, получим: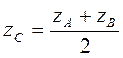 
.
Решение задач
1. Какие координаты середины С отрезка АВ, если А(0; 2; -11), В (2; 0; -1)? (Ответ. С(1;1;-6).)
2. Дано С(2; 6; 3), А(4; 2; 1). Найдите координаты точки В, если известно, что АС = ВС и точки А, В, С лежат на одной прямой. (Ответ. В(0;10;5).)
3. Найдите координаты середин сторон треугольника АВС, если А(2; 0; 2), В(2;2;0), С(2;2;2). (Ответ. A1(2; 2; 1), B1(2; 1; 2), C1(2; 1; 1).)
4. Найдите длину медианы AM треугольника АВС, если А (2; 1; 3), В(2; 1; 5), С(0; 1; 1). (Ответ. AM = 1.)
5. Задача № 9 из учебника (с. 55).
6. Задача № 13 (3) из учебника (с. 55)
7. Задача № 15 из учебника (с. 55).
8. Точки М(-2; 3; 4), N(3; 5; 2) и К(3; -5; 1) - середины сторон треугольника. Найдите координаты вершин этого треугольника.
(Ответ. (-2; -7; 3), (-2; -13; 5), (8; -3; -1).)
9. Если А (хA; A; zA), В(хB; B; zB) C (xC; C; zC) - координаты вершин треугольника, то М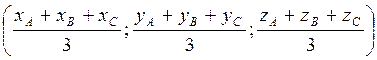
- точка пересечения медиан треугольника. Довести.
III. Домашнее задание
§4, п. 25; контрольный вопрос № 3; задачи№ 10 (1), 11 (1), 12, 13 (1) (с. 55).
IV. Подведение итога урока
При подведении итога урока можно воспользоваться данной стенной таблицей.
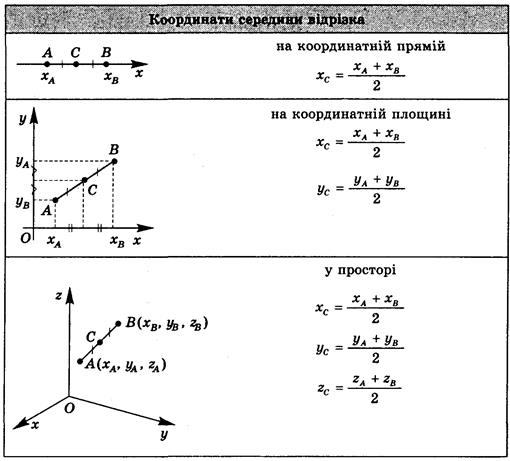
Вопрос к классу
1) Как найти координату середины отрезка, концы которого лежат на координатной прямой?
2) Как найти координаты середины отрезка, концы которого лежат в координатной плоскости?
3) Как найти координаты середины отрезка, заданного в пространстве?