Урок № 34
Тема. Сумма углов треугольника
Цель: закрепить знания
учащихся о содержании теоремы о сумме углов треугольника и следствий из нее; работать
над усвоением понятия «внешний угол треугольника»; рассмотреть свойство
внешнего угла треугольника.
Сформировать умения:
·
находить
на рисунке и выполнять изображение внешнего угла при данной вершине
треугольника;
·
записывать
теорему о внешний угол треугольника согласно условия задачи;
·
использовать
свойство внешнего угла треугольника вместе с теоремой о сумме углов
треугольника для решения задач, предусмотренных программой.
Тип урока: применение знаний,
умений и навыков.
Наглядность и
оборудование: набор
демонстрационного чертежных принадлежностей; таблица «Внешний угол треугольника».
ХОД УРОКА
I. Организационный
момент
II. Проверка
домашнего задания
Как вариант
проверки усвоенных знаний и умений можно предложить самостоятельную работу.
Самостоятельная работа
Вариант 1
Начальный уровень
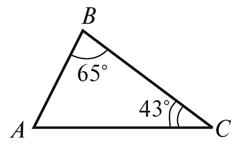
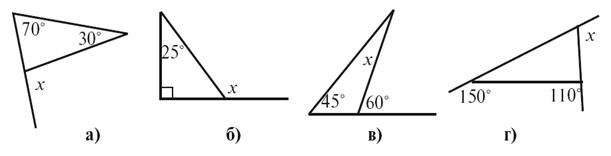
1. Найдите неизвестный
угол треугольника (рис. 1).
Средний
уровень
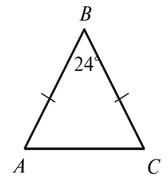
2. Найдите неизвестные
углы треугольника (рис. 2).
Вариант
2
Начальный уровень
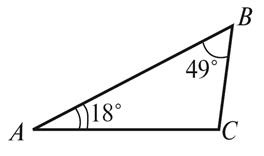
1. Найдите неизвестный
угол треугольника (рис. 3).
Средний
уровень
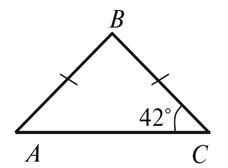
2. Найдите неизвестные
углы треугольника (рис. 4).
III. Мотивация
учебной деятельности. Формулировка цели и задач урока
Для создания
соответствующей мотивации деятельности учащихся можно предложить им выполнить упражнение.
Упражнение.
Начертите
произвольный треугольник ABC (или вариант 1: остроугольный Δ ABC;
вариант 2:
прямоугольный Δ ABC; вариант 3: тупоугольный Δ ABC).
а) Проведите
луч BD, доповняльний до луча BA. Которыми являются углы ABC и DBC, при этом
образовались?
б) Измерьте углы
треугольника ABC и угол DBC. Сравните градусные меры углов: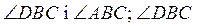 
и суммы 
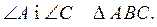Что вы заметили?
До выполненного
задание учитель или ученики формулируют вопрос: всегда ли можно построить угол DBC
и сколько их можно построить? Будет выполняться соотношение между углом DBC
и суммой углов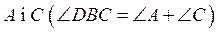 
в
будь_якому треугольнике?
Поиск ответов на
эти вопросы и являются, по сути, основной целью урока.
IV. Актуализация
опорных знаний
Выполнение
устных упражнений
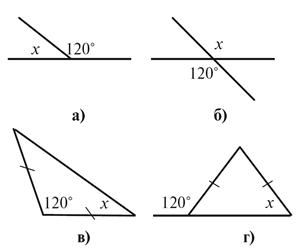
1. Найдите градусную
меру угла x (рис. 5).
2.
Или
существует треугольник с двумя:
а) тупыми углами;
б) прямыми углами?
3. Существует ли треугольник,
все углы которого:
а) острые, меньше
60°;
б) острые, большие
при 60°?
V. Усвоение новых знаний
План изучения
нового материала
1°. Определение
внешнего угла треугольника.
2°. Теорема о
свойство внешнего угла треугольника.
3°. Следствие из теоремы
о внешний угол треугольника.
Методический комментарий
Введение понятия
внешнего угла треугольника подготовлено выполнением практической работы, поэтому,
дав определение, можно предложить несколько готовых рисунков (как примеров, так
и контрпримеров), на которых изображен внешний угол треугольника и угол, который не является
внешним. При этом следует обратить внимание на возможность построения двух (уровне между
собой как вертикальные) внешних углов при каждой вершине треугольника. Также
обращаем внимание учащихся на технологию построения внешнего угла треугольника.
Как
результат изученного материала учащиеся составляют таблицу.
VI. Первичное осознание
нового материала
Выполнение
устных упражнений
1. Для Δ ABC постройте
внешние углы при вершине C.
2. Угол B треугольника ABC
равен 140°. Чему равен внешний угол при Вершине B?
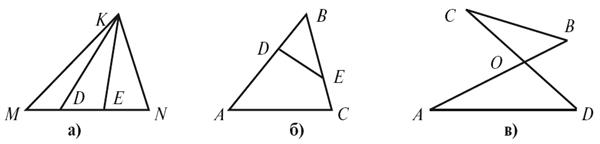
3.
Назовите
внешние углы:
а) при вершинах D и
E треугольника DKE (рис. 2 а);
б) при вершине E треугольника
ΔKEN (рис. 2 а);
в) при вершинах D и
E треугольника DBE (рис. 2 б);
г) при вершине треугольника O
AOD (рис. 2 в).
4.
Найдите
угол x на рисунке 3 (рациональным способом):
VII. Усвоение
умений
Задачи, которые надо
решить на уроке, условно разделим на три группы.
И
группа. Задачи
на применение теоремы о внешний угол треугольника.
1. Найдите внутренние
углы треугольника, если внешние углы при двух его вершинах равны 135° и
110°.
2. Один из внешних
углов равнобедренного треугольника равен 60°. Найдите внутренние углы
треугольника.
II
группа. Задачи
на последствия применения теоремы о внешний угол треугольника.
Внешние углы
треугольника относятся как 3 : 4 : 5. Найдите внутренние углы треугольника.
III
группа. Задачи
на применение теоремы о сумме углов треугольника и внешний угол.
Уровень Б
В рівнобедреному
треугольнике ABC с основанием AC проведена бісектрису AD. Найдите углы данного
треугольника, если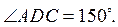 
Уровень В
1. Биссектриса
равнобедренного треугольника, проведенная из вершины угла при основании равна основе
треугольника. Найдите его углы.
2. Биссектриса
внешнего угла при основании равнобедренного треугольника пересекает продолжение
боковой стороны. Длина отрезка биссектрисы от начала до точки пересечения
равной основе треугольника. Найдите внутренние углы треугольника.
VIII. Итоги урока
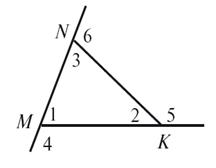
Для углов
треугольника MNK, изображенного на рисунке 4, записать как можно больше правильных
равенств (проводим «аукцион»).
IX. Домашнее
задача
Изучить теоретический
материал.
Выполнить устно
упражнение.
Дано три внешние
углы треугольника при разных вершинах. Сколько из них могут быть острыми?
Выполнить графическую
упражнение.
Начертите
остроугольный треугольник ABC.
а) Измерьте углы
треугольника и вычислите их сумму.
б) На луче AC отметьте
точку D, которая не принадлежит отрезку AC. Определите градусную меру угла BCD,
пользуясь теоремой о внешний угол треугольника.
в) Определите вид
треугольника BCD по величине углов.
Письменно
решить задачи.
1. Один из внутренних
углов треугольника равен 40°, а один из внешних - 125°. Найдите остальные
внутренних и внешних углов.
2. Найдите внутренние
углы треугольника, если сумма двух из них равна 150°, а один из внешних углов
равен 80°.
Источники:
1. Уроки геометрии. 7 класс./ С. П. Бабенко
- Х.: Изд. группа «Основа», 2007.- 208 с.