Урок № 33
Тема. Сумма углов треугольника
Цель: добиться усвоения
учащимися содержания теоремы о сумме углов треугольника и схемы ее доведения, а также
следствий из теоремы.
Сформировать умение
учащихся:
·
воспроизводить
формулировка указанной теоремы и ее последствий;
·
применять
эти утверждения при решении задач на нахождение неизвестных углов
треугольника.
Тип урока: усвоение знаний.
Наглядность и
оборудование: набор
демонстрационного чертежных принадлежностей; таблица «Сумма углов треугольника и
последствия».
Таблица

ХОД УРОКА
I. Организационный
момент
II. Проверка
домашнего задания
Если домашним
задачей было выполнение домашней самостоятельной работы, то учитель собирает тетради
на проверку и при необходимости делает некоторые пояснения к задачам (или раздает
решения задач для самостоятельной проработки).
III. Мотивация
учебной деятельности. Формулировка цели и задач урока
Для успешной
мотивации деятельности учащихся учитель побуждает учащихся к повторению основных
сведений о треугольнике (как одну из основных геометрических фигур) и ставит
проблему: что ученики знают об углы треугольника? Как один из вариантов ответа: в
треугольнике не может быть два прямых угла (см. теорему о существовании и единстве
прямой, перпендикулярной к данной прямой, проходящей через данную точку).
Основная
цель (формулирует учитель) - использовав сведения о свойстве углов при
параллельных прямых, сформулировать и доказать свойство углов треугольника и
последствия, вытекающие из этого свойства.
IV. Актуализация
опорных знаний
Выполнение
устных упражнений
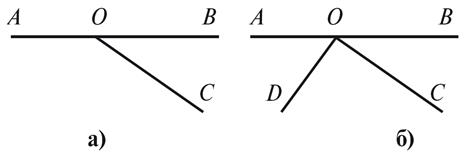
1. Есть ли на рисунке 1 пара
смежных углов? Назовите их.
2.
На
рисунке 2 назовите равные углы треугольников.
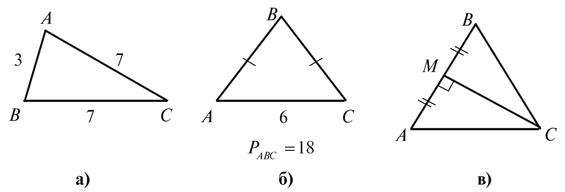
3.
Вставьте
пропущенные рисунки и записи:
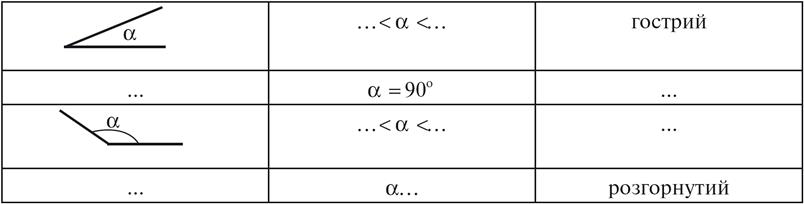
V. Усвоение новых
знаний
План изучения
нового материала
1°. Теорема о сумме
углов треугольника (с доказательством).
2°. Следствия из теоремы
о сумме углов треугольника.
3°. Классификация
треугольников по величине углов.
Методический комментарий
Если позволяет
подготовка учеников, то работу по изучению теоремы можно организовать в виде
небольшой практической работы.
1. На рисунке 3 назовите
пары внутренних разносторонних углов при прямых a и b и секущих AB и BC.
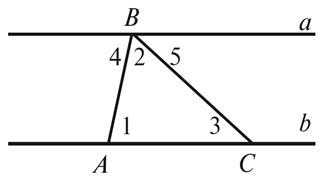
2.
Что
можно сказать про углы каждой пары (см. выше), если a||b?
3. Найдите на рисунке
3 смежные углы с вершиной в точке B. Чему равна их сумма?
4. Сравните сумму
смежных углов (см. выше) с суммой углов треугольника. Сделайте вывод.
Для подготовки к
восприятия следствия 1 можно предложить учащимся вопрос:
Могут ли быть в
треугольнике:
а) две прямые углы;
б) два угла 100° и
120°;
в) две тупые углы;
г) один угол тупой,
а другой - прямой?
Если ученики дают
ответы с обоснованием, то доказательство следствия 1 будет иметь вид
обобщение проведенных рассуждений.
Как квинтэссенция
работы по изучению нового материала демонстрируется таблица «Сумма углов
треугольника».
Вопрос о видах
треугольников по величине углов не является новым для семиклассников. Поэтому, побудив
их к воспроизведению знаний, приобретенных в 5 классе, учитель имеет только акцентировать внимание
учащихся на научном содержании понятия «классифицировать» и на необходимых условиях
правильной классификации.
VI. Первичное
осознание нового материала
Задачи, вынесено
на урок, можно условно разделить на три группы.
И
группа. Задачи
на непосредственное применение теоремы.
Уровень А
Найдите неизвестный
угол треугольника, если два его угла равны: а) 65° и 45°; б) 120° и 18°; в)
90° и 64°.
Уровень Б
Найдите все углы
треугольника, если:
а) один из них
вдвое меньше второй и на 20° больше третий;
б) их градусные
меры относятся как 1 : 3 : 5.
II
группа. Задачи
на применение теоремы о сумме углов треугольника вместе со свойством углов
равнобедренного треугольника.
Уровень А
Найдите неизвестные
углы равнобедренного треугольника, если:
а) угол при его
основе равен 40°;
б) угол, противоположный
его основе, равен 40°.
Уровень Б
Один из углов
равнобедренного треугольника равен 50°. Найдите остальные углы. Сколько
решений имеет задача?
III
группа. Задачи
на применение следствий из теоремы.
Уровень А
Докажите методом
от противного, что угол при основании равнобедренного треугольника не может быть
тупым.
Уровень В
Может ли треугольник
с углом 40° равняться треугольнике с углом 140°? Ответ обоснуйте.
Приведены задачи
уровня А можно решить устно, для этого учителю достаточно заранее сделать
рисунки и обозначить на них известные величины.
VII. Итоги урока
Какое из утверждений (рис.
4) неправильное?
1) 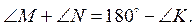
2) 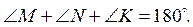
3) Если 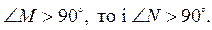
4) Если 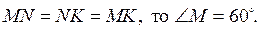
VIII. Домашнее
задача
Изучить теоретический
материал.
Выполнить устные
упражнения.
1. Может ли треугольник
иметь три тупые углы; два тупые углы; не иметь ни одного тупого угла?
2. Может ли угол при
основании равнобедренного треугольника быть тупым? прямым?
3. Может ли прямоугольный
треугольник быть равнобедренным? равносторонним?
Выполнить
графическую упражнение.
Начертите
треугольник ABC с тупым углом A.
а) Проведите высоту
BD и определите вид треугольника ABD по величине углов.
б) Измерьте угол BAD.
Как связана его градусная мера с градусными мерами углов треугольника ABC?
Письменно решить
задачу.
Найдите:
а) углы треугольника,
если их градусные меры относятся как 2 : 7 : 9;
б) углы равнобедренного треугольника, если
один из них равен 100°.
Источники:
1. Уроки геометрии. 7 класс./ С. П. Бабенко
- Х.: Изд. группа «Основа», 2007.- 208 с.