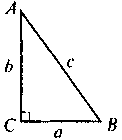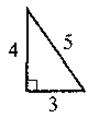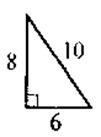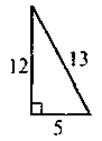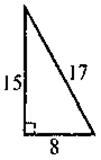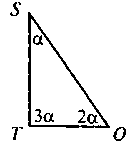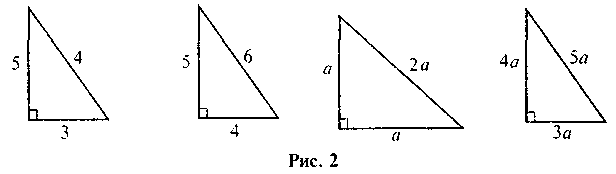Урок № 34

Тема. Теорема Пифагора

Цель: сформировать у учащихся понимание содержания теоремы Пифагора и ее доказательства. Формировать умение воспроизводить содержание теоремы Пифагора, применять ее формулировка для решения задач на нахождение неизвестных сторон прямоугольных треугольников.

Тип урока: усвоение новых знаний.

Наглядность и оборудование: конспект «Теорема Пифагора».

Ход урока

I. Организационный этап

II. Проверка домашнего задания

Во время устного обсуждения контрольных моментов решения домашних задач ученики должны воспроизвести аргументированные рассуждения с использованием признаков подобия прямоугольных треугольников и метрических соотношений в прямоугольном треугольнике.

Обсуждение решения задачи 4 способствует повторение опорного факта: медиана прямоугольного треугольника, проведенная к гипотенузу, делит:

· данный треугольник на два равнобедренных треугольников, основаниями которых являются катеты данного треугольника;

· прямой угол прямоугольного треугольника на две кучи, равным острым углам данного прямоугольного треугольника.

III. Формулировка цели и задач урока

Для осознания учащимися важности материала, который будет изучаться на уроке, предлагаем им решить задачу.

Задача. Можно ли прямоугольник со сторонами 6 см и 8 см вписан в окружность с радиусом 5 см?

Чтобы найти ответ на вопрос задачи, ученики должны составить математическую модель задачи, которая имеет следующий вид: найти диагональ прямоугольника со сторонами 6 см и 8 см найти гипотенузу прямоугольного треугольника с катетами 6 см и 8 см. Анализ ситуации приводит учащихся к осознанию невозможности (или нерациональности) решение задачи средствами, которыми овладели учащиеся на предыдущих этапах изучения геометрии. Таким образом, констатируется необходимость расширения знаний учащихся относительно соотношений в прямоугольном треугольнике. Поэтому задача на урок формулируется так: опираясь на известные ученикам соотношения в прямоугольном треугольнике, сформулировать утверждение, которое выражает зависимость между сторонами прямоугольного треугольника, доказать его. А также сформировать умение применять эти зависимости для нахождения неизвестных сторон прямоугольного треугольника.

IV. Актуализация опорных знаний

С целью успешного усвоения учащимися содержания теоремы Пифагора и ее доказательства ученикам следует активизировать знания и умения по определение прямоугольного треугольника; метрических соотношений в прямоугольном треугольнике.

Выполнение устных упражнений по готовым рисункам

V. Усвоение знаний

План изучения нового материала

1. Теорема Пифагора: доказательства и формулировки.

2. Примеры применения.

@ В отличие от предыдущих лет, когда доказательство теоремы Пифагора осуществлялось со ссылкой на свойства косинуса острого угла прямоугольного треугольника, в новом учебнике теорема Пифагора очень просто приходится со ссылкой на метрические соотношения в верхнем треугольнике. Поэтому доказательство теоремы Пифагора можно провести в следующем порядке:

· рассмотреть прямоугольный треугольник с катетами а и b, гипотенузой с и высотой, проведенной к гипотенузы hc;

· для него треугольника записать метрические соотношения для катетов;

· выполнить почленне добавление обеих частей полученных равенств;

· преобразовать правую часть полученного равенства, используя аксиому измерения отрезков.

После получения искомой равенства учитель предлагает ученикам «перевести» ее с математического языка на обычный. Таким образом ученики формулируют утверждение теоремы Пифагора.

В завершение изучения материала как пример на применение теоремы учащиеся решают задачу, с которой началось изучение материала на уроке: найти гипотенузу, если катеты равны 6 см и 8 см (c2 = 62 + 82 = 100, с = 10). Таким образом демонстрируется практическое значение изученной теоремы.

Напоследок можно подчеркнуть, что из теоремы Пифагора вытекает свойство, изучается в 7 классе: гипотенуза данного прямоугольного треугольника всегда больше его катет.

При рассмотрении примеров решения задач на применение теоремы Пифагора по учебнику следует проверить соответствие знаний учащихся относительно содержания понятия квадратный корень. Так же в отборе задач к уроку следует помнить о необходимости соблюдения соответствия между геометрическим и алгебраическим материалом.

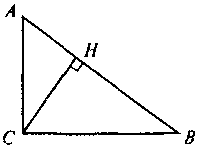
VI. Формирование первичных умений

Выполнение устных упражнений

1. Для каких треугольников, изображенных очерк. 1, выполняется теорема Пифагора? Выполните соответствующие записи.

Рис. 1

2. «Мне удалось построить прямоугольный треугольник, у которого длины всех сторон - целые нечетные числа», - сказал ученик. Докажите, используя теорему Пифагора, что он ошибся.

3. В ромбе известны сторона и одна из диагоналей. Как найти другую диагональ ромба, не пользуясь рисунком?

4. 1) Катеты прямоугольного треугольника 5 см и 12 см. Найдите гипотенузу.

2) Гипотенуза треугольника 5 см, а один из катетов равен 3 см.

Найдите второй катет.

3) Катеты прямоугольного треугольника относятся как 3 . 4, а гипотенуза равна 15 см. Найдите периметр треугольника.

4) Периметр квадрата равен 4 см. Найдите диагональ квадрата.

5) Определите вид треугольника ABC, если: 1) АС = 5, ВС = 6 , АС = 7; 2) АС = 4. ВС = 2, AC = 6.

Выполнение графических упражнений

Начертите прямоугольный треугольник с катетами 3 см и 4 см. Вычислите по теореме Пифагора длину его гипотенузы. Проверьте результат измерением.

Выполнение письменных упражнений

1. В прямоугольном треугольнике с катетами а и b и гипотенузой с найдите с, если а = 7, b = 24 .

2. В прямоугольнике найдите периметр, если диагональ равна 10 см, а одна из сторон - 6 см.

3. Основа равнобедренного треугольника равна 16 см. Найдите периметр треугольника, если биссектриса, проведенная к основанию, равна 6 см.

4. В прямоугольном треугольнике найдите неизвестные стороны, если:

а) катеты относятся как 3 : 4. а гипотенуза равна 45 см;

б) разность между гипотенузой и катетом равен 1 см, а второй катет равен 5 см;

в) высота, проведенная к гипотенузу, равна 12 см, а проекция одного из катетов на гипотенузу имеет длину 16 см.

5. Основы рівнобедреної трапеции равны 8 см и 18 см, а высота 12 см. Найдите периметр трапеции. Можно ли вписать в него круг?

6. Две большие стороны прямоугольного треугольника равны 65 см и 63 см. Найдите третью сторону.

Поскольку на уроке начинается работа по формированию умений применять теорему Пифагора, то нужно сразу вырабатывать у учащихся навыки математической культуры, то есть применению теоремы Пифагора для некоторого прямоугольного треугольника должны предшествовать следующие соображения:

Рассмотрим треугольник..., в нем угол... - прямой, следовательно, треугольник прямоугольный с гипотенузой... Поэтому по теореме Пифагора... (делается общая запись теоремы для данного прямоугольного треугольника).

Только после этого возможно выполнение вычислений, составление уравнения, выражения неизвестных т.д. (Впоследствии эти рассуждения можно будет сокращать, но на первом уроке этого делать не следует).

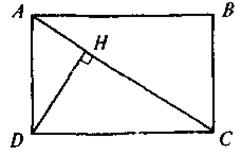
VII. Итоги урока

На каком из рисунков (см. рис. 2) допущены ошибки в изображении прямоугольного треугольника?

VIII. Домашнее задание

Изучить содержание и доказательства теоремы Пифагора.

Решить задачи.

1. В прямоугольнике найдите диагональ, если стороны равны 10 см и 24 см.

2. Периметр равнобедренного треугольника равен 36 см, а боковая сторона - 13 см. Найдите медиану треугольника, проведенную к основанию.

3. В прямоугольном треугольнике найдите неизвестные стороны, если:

а) катет и гипотенуза относятся как 12 : 13, а второй катет равен 10см;

б) катет больше своей проекции на гипотенузу на 8 см, а высота, проведенная к гипотенузу, равна 24 см.

4. Основания прямоугольной трапеции равны 21 см и 28 см, а большая боковая сторона - 25 см. Найдите периметр трапеции. Можно ли вписать в него круг?