Урок № 35

Тема. Теорема, обратная теореме Пифагора

Цель: добиться сознательного понимания учащимися содержания теоремы Пифагора и ее доказательства: сформировать понятие египетского треугольника, пифагоровой тройки чисел, пифагоровых треугольников. Формировать умение воспроизводить содержание изученной теоремы и применять ее при решении задач на доказательство.

Тип урока: усвоение новых знаний.

Наглядность и оборудование: конспект «Теорема Пифагора».

Ход урока

I. Организационный этап

II. Проверка домашнего задания

Усвоение учащимися содержания теоремы Пифагора и первичных умений ее использования проверяем, проведя математический диктант.

Математический диктант

Решение письменных упражнений проверяем во время устной работы с готовыми рисунками этих задач.

III. Формулировка цели и задач урока

Создать положительную мотивацию познавательной деятельности учащихся можно, проведя этот этап урока в игровой форме.

Игра «Что? Где? Когда?»

Вопрос знатокам

Древние египтяне строили прямые углы на местности таким образом: делили узлами веревку на 12 равных частей, связывали ее конце, после чего веревку растягивать на земле так, чтобы образовался треугольник со сторонами 3, 4 и 5 делений. Угол треугольника, лежащий против стороны с 5-ю делениями, был прямой. Можете ли вы обосновать правильность этого построения или опровергнуть ее?

В результате поиска ответов па вопросы ученики должны понять, что с математической точки зрения вопрос ставится как определение того, будет ли треугольник со сторонами 3, 4, 5 единиц прямоугольным. Также ученики должны понять, что применение теоремы Пифагора для решения задачи невозможно (потому что в условии нет утверждения, что треугольник является прямоугольным).

Таким образом формулируется общая проблема: как, не проводя измерений, определить, с треугольник с заданными длинами (соотношением сторон прямоугольным, - решение которой и является основной целью урока.

IV. Актуализация опорных знаний

С целью успешного усвоения учащимися содержания теоремы, обратной теореме Пифагора, и доведение ее ученикам следует активизировать знания и умения по определение прямоугольного треугольника; признаки равенства треугольников; теоремы Пифагора.

Выполнение устных упражнений

1. Дано: M = B = 90°, МС = ВС (рис. 1). Докажите, что АВ = МН.

2. Дано: AB AD, CD AD,1 = 2 (рис.2).Доведіть, что ΔABD = ΔDCA.

3. Диктант.

1) Если катеты прямоугольного треугольника равны 12 см и 9 см, то гипотенуза равна...

2) Если две большие стороны прямоугольного треугольника равны 17 и 15, то третья сторона равна...

3) Если диагональ квадрата равна 12 см, то сторона квадрата имеет длину...

4) Если диагонали ромба имеют длины 12 см и 16 см, то сторона ромба имеет длину.

V. Усвоение знаний

План изучения нового материала

1. Теорема, обратная теореме Пифагора: формулировка и доказательство.

2. Египетский треугольник.

3. Пифагоровы тройки чисел, пифагоровы треугольники.

@ Материал, вынесенный для изучения на урок, до недавнего времени содержался в учебнике в виде опорной задачи. По новой программе по математике среди программных требований знание теоремы, обратной теореме Пифагора, и умение доказывать ее, также отдельно не выделены. Однако решение многих задач, связанных с прямоугольным треугольником, базируется именно на применении этой теоремы. Поэтому, изучив теорему Пифагора, учащиеся имеют по крайней мере ознакомиться с содержанием и доведением обратной теоремы, а также сформировать умение применять ее для определения вида треугольника с заданными длинами сторон.

Содержание материала п. и 3.2, что содержится после доказательства теоремы, не является обязательным для изучения всеми учащимися, однако, учитывая то, что в задачах довольно часто фигурируют именно пифагоровы треугольники, знание этого понятия, а также знания учащимися нескольких пифагоровых троек (наиболее часто встречаются тройки: 3, 4, 5; 5, 12, 13; 6, 8, 10; 8, 15, 17) может помочь учащимся существенно упростить вычисления неизвестных сторон треугольников. (Для учащихся, которые интересуются математикой, предлагаются формулы для сборки пифагоровых троек.)

Если m и n - натуральные числа, то числа 2mn, m2 - n2 и m2 + n2 составляют пифагоровы тройки. Докажите.

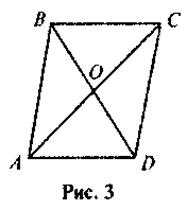
VI. Формирование первичных умений

С целью закрепления знаний учащихся относительно содержания теоремы, обратной теореме Пифагора, а также формирование умений применения утверждение этой теоремы к решению задач, ученики должны последовательно решить устные задачи.

Выполнение устных упражнений

1. Правильно ли определен вид треугольника?

а) Поскольку 122 ≠ 132 + 52, то треугольник со сторонами 5, 12, 13 не является прямоугольным;

б) поскольку 6 = 5 + 1, то сторона длиной 6 единиц лежит против прямого угла.

2. Определите вид треугольника ABC, если:

1) АС = 5, ВС = 6, АС = 7;

2) АС = 4, BC = 2, AC = 6.

3. Какую градусную меру имеет наибольший угол треугольника со сторонами 6, 8 и 10? Почему?

4. Стороны параллелограмма равны 3 см и 4 см, а диагональ - 5 см. Определите вид параллелограмма.

5. Правильно ли сделан рисунок 3 такая запись: «Дано АВ = 5 см, BD = 4 см, АС = 6 см, ABCD -параллелограмм»?

Выполнение графических упражнений

Постройте треугольник со сторонами 2,5 см, 6 см и 6,5 см. Измерьте наибольший угол треугольника. Подтвердите полученный результат с Помощью теоремы, обратной теореме Пифагора.

Выполнение письменных упражнений

1. Определите, является ли прямоугольным треугольник со сторонами:

а) 4, 5, 6;

б) 2, , .

2. Диагонали параллелограмма равны 16 см и 30 см, а сторона - 17 см. Докажите, что данный параллелограмм является ромбом.

3. Стороны треугольника равны 15 см, 20 см и 25 см. Найдите медиану и высоту, проведенную к наибольшей стороны.

4. Найдите высоты треугольника, если его стороны равны 7 см, 24 см и 25 см.

Кроме того, на уроке следует выделить время для решения задач на применение теоремы Пифагора.

Выполнение письменных упражнений

1. В рівнобедреному прямоугольном треугольнике найдите:

а) гипотенузу, если катет равен 4 см; 2 см; см;

б) катет, если гипотенуза равна 10 см; см; с см.

2. Две стороны прямоугольного треугольника равны 6 см и 8 см. Найдите длину третьей стороны. Сколько решений имеет задача?

3. В равностороннем треугольнике найдите высоту, если сторона равна 6 см; 2 см; а см.

4. Высота равнобедренного треугольника делит боковую сторону на отрезки длиной 1 см и 12 см, начиная от основания. Найдите основание треугольника.

@ При решении залам на прямое применение теоремы, обратной теореме Пифагора (см. устные упражнения № 2, 3), следует требовать от учеников предварительного воспроизведения содержания теоремы с последующей записью соответствующей равенства и проверкой правильности полученного равенства.

Также на уроке продолжается формирование умений применять теорему Пифагора. Поэтому, чтобы избежать путаницы, следует заметить ученикам, что изученные теоремы имеют различные сферы применения: теорема Пифагора применяется в случае, когда по условию задачи дано прямоугольный треугольник (или существования прямоугольного треугольника обусловлено свойствами фигур, данных в условии - см. свойства четырехугольников и понятие высоты треугольника); обратная теорема используется в случае, когда условие задачи содержит длины сторон некоторого треугольника (абсолютные значения или в виде выражений или отношений) и условию задачи требуется определить, является ли треугольник прямоугольным.

Также следует обратить внимание на задачи №1,3 (письменные упражнения) - в задачах выводятся формулы, которые полезно зафиксировать в конспектах учащихся как опорные.

Гипотенуза прямоугольного равнобедренного треугольника с катетом а вычисляется по формуле с = а; высота равностороннего треугольника со стороной а вычисляется по формуле .

VII. Итоги урока

Две стороны треугольника имеют длины 4 см и 5 см. Какой может быть длина третьей стороны, чтобы этот треугольник был прямоугольным? Пифагоровым?

VIII. Домашнее задание

Изучить содержание основных понятий урока.

Решить задачи.

1. В квадрате найдите:

а) диагональ, если сторона равна а;

б) сторону, если диагональ равна d .

2. Стороны треугольника равны 12 см, 16 см и 20 см. Какой угол образует с наименьшей стороной биссектриса наибольшего угла?

3. В равностороннем треугольнике найдите сторону, если высота равна 1 см; 3 см: h см.

Повторить определение перпендикуляра к прямой, теорему Пифагора, свойства сторон прямоугольного треугольника.
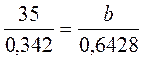
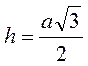