УРОК № 34

Тема. Симметрия относительно точки

Цель урока: формирование понятия симметрии относительно точки; изучение свойств симметрии относительно точки; формирование умений применять изученные определения и свойства к решению задач.

Тип урока: комбинированный.

Наглядность и оборудование: таблица «Преобразование фигур. Движения» [13].

Требования к уровню подготовки учащихся: описывают симметрию относительно точки; строят фигуры, в которые переходят данные фигуры при симметрии относительно точки; приводят примеры фигур, имеющих центр симметрии; применяют изученные определения и свойства к решению задач.

Ход урока

I. Проверка домашнего задания

Проверить наличие выполненных домашних заданий и ответить на вопросы, которые возникли у учащихся при их выполнении.

Фронтальное опрос

1. 1) Какое преобразование фигуры называется перемещением?
2. 2) Докажите, что во время движения точки, лежащие на прямой, переходят в точки, также лежащие на прямой, и сохраняется порядок их взаимного расположения.
3. 3) Во что переходят прямые, півпрямі, отрезки при перемещении?
4. 4) Докажите, что при перемещении сохраняются углы.
5. 5) Периметры двух ромбов уровне. Следует ли из этого, что и ромбы уровне?
6. 6) Периметры двух квадратов уровне. Ровные квадраты?

II. Поэтапное восприятие и осознание нового материала

Понятие симметрии относительно точки

Преобразования фигур с помощью перемещения имеет несколько видов. Сегодня мы ознакомимся с преобразованием фигуры с помощью симметрии относительно точки.

Точки X и X1 называются симметричными относительно точки О, если точка О является серединой отрезка ХХ1 (рис. 160).

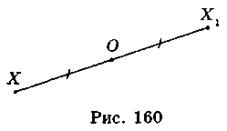
Точка О называется центром симметрии. Преобразование фигуры F в фигуру Ft, при котором каждая точка X фигуры F переходит в точку Х1 фигуры F1, симметричную точке X относительно данной точки О, называется преобразованием симметрии относительно точки О. Фигуры F и F1 называются центральносиметричними (симметричными относительно точки О) (рис. 161).

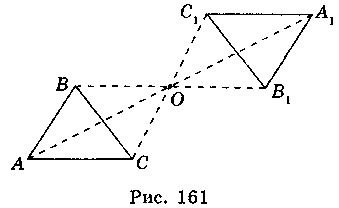
Свойства симметрии относительно точки (центральная симметрия)

1. 1) Преобразование симметрии относительно точки является перемещением.
2. 2) Преобразование симметрии относительно точки превращает прямую на параллельную ей прямую или на себя; отрезок - на равный и параллельный ему отрезок; многоугольник - на равный ему многоугольник.
3. 3) Любая прямая, проходящая через центр симметрии, отображается при этой симметрии на себя. Если преобразование симметрии относительно точки О переводит фигуру F (рис. 162) в себя, то она называется центральносиметричною, а точка О - центром симметрии.

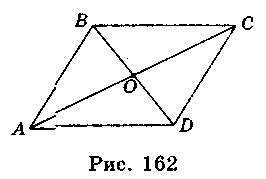
Если точка А(х;у) симметрична точке В(х1; у1) относительно начала координат О, то выполняются условия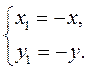

Выполнение упражнений

1. 1. Постройте произвольный треугольник ABC. Постройте треугольник, симметричный построенном относительно точки:

а) А;

б) В;

в) которая лежит снаружи треугольника;

г) которая лежит внутри треугольника.

1. 2. Постройте четырехугольник ABCD, у которого А(1; 1), В(-1; 1), С(1; 3) и D(-1; 3). Постройте четырехугольник, симметричный построенном четырехугольнике относительно точки О.

III. Закрепление и осмысление учебного материала
Выполнение упражнений

1. 1. Докажите свойства симметрии относительно точки.
2. 2. Запишите уравнение окружности, которое симметричное окружности (х - 1)2 + (у + 2)2 = 1 относительно начала координат.
3. 3. Запишите уравнение прямой, которая симметрична прямой х + у = 1 относительно начала координат.
4. 4. Даны две прямые, которые пересекаются, и точка О, лежащая между ними. Постройте отрезок с концами на данных прямых и серединой в данной точке.

IV. Домашнее задание

1. 1. Изучить теоретический материал.
2. 2. Решить задачи.
3. 1) Докажите, что у параллелограмма точка пересечения диагоналей является центром симметрии.
4. 2) Докажите, что четырехугольник, у которого есть центр симметрии, является параллелограммом.

V. Подведение итогов урока

Вопрос к классу

1. 1. Какие точки называются симметричными относительно данной точки?
2. 2. Какие преобразования называются симметрией относительно данной точки?
3. 3. Какая фигура называется центральносиметричною?
4. 4. Что такое центр симметрии фигуры? Приведите примеры центральносиметричних фигур.