УРОК № 33

Тема. Перемещения и его свойства. Равные фигуры

Цель урока: формирование понятия перемещения и равных фигур; изучение свойств перемещения.

Тип урока: комбинированный.

Наглядность и оборудование: таблица «Преобразование фигур». Движения» [13].

Требования к уровню подготовки учащихся: описывают равенство фигур; строят фигуры, в которые переходят данные фигуры при перемещениях; формулируют свойства перемещения; применяют изученные определения и свойства к решению задач.

Ход урока

И. Проверка домашнего задания, актуализация опорных знаний учащихся

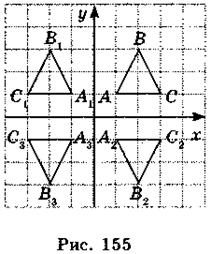
1. 1. Правильность выполнения домашнего задания проверить с записями, сделанными на доске до начала урока (рис. 155).
2. 2. Фронтальная беседа
3. 1) Объясните, что такое преобразование фигуры F в фигуру F1.
4. 2) Приведите примеры преобразования фигур.

II. Поэтапное восприятие и осознание нового материала

Понятие перемещения и равных фигур

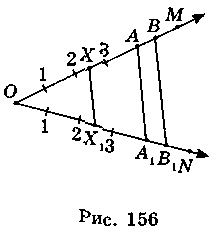
Рассмотрим два отрезка ОМ и ON, которые имеют одинаковую длину (рис. 156). Зададим преобразование отрезка ОМ на отрезок ON. Для этого на прямых ОМ и ON введем координаты, выбрав одинаковые единичные отрезки и общее начало координат О (выбрав положительный направление - лучи ОМ и ON). Поставим в соответствие каждой точке X отрезка ОМ точку X отрезка ON, которая имеет ту же координату, что и точка X. Получим преобразование отрезка ОМ на отрезок ON. Для любых точек А и В отрезка ОМ расстояние между образами А и В равна АВ.

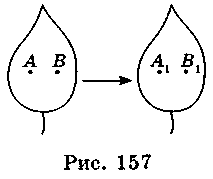
Преобразование одной фигуры на другую называют перемещением или движением, если оно сохраняет расстояние между точками, т.е. переводит любые две точки А и В первой фигуры в точки А1 и В1 второй фигуры так, что АВ = А1В1 (рис. 157).

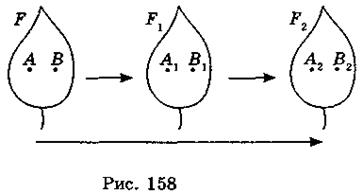
Два перемещения, выполненные последовательно, дают снова перемещения (рис. 158). Если фигура F переводится перемещением в фигуру F1, а фигура F1 переводится перемещением в фигуру F2, то преобразование фигуры F в фигуру F2 также является перемещением.

Если преобразование переводит фигуру F в фигуру F1, то существует преобразование, которое переводит фигуру F1 в фигуру F, которое называется обратным к данному. Преобразование, обратное перемещение, также является перемещением.

Две фигуры называются равными, если они переводятся перемещением друг в друга.

Докажем теорему: при перемещении точки, лежащие на прямой, переходят в точки, лежащие на прямой, и порядок их взаимного расположения сохраняется.

Доведение

Пусть на прямой АВ точка С (рис. 159) лежит между точками А и В, а точки A1, B1, C1 - образы точек А, В, С, полученные в результате перемещения. Докажем, что точка С1 лежит на прямой A1B1 между точками А1 и В1.

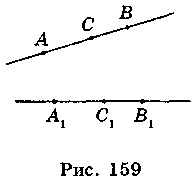
Если точка С лежит между точками А и В, то АВ = АС + СВ. По определению перемещения АВ = А1В1, АС = A1С1, СВ = С1В1, следовательно, А1В1 = A1С1 + C1B1, а это означает, что точка С1 лежит между точками A1 и В1, т.е. точки А1? В1, С1 лежат на одной прямой.

Свойства перемещения

Из последней теоремы следует, что при перемещении:

а) прямые переходят в прямые;

б) лучи - лучи;

в) отрезок - в отрезок;

г) сохраняются углы между лучами;

д) півплощина переходит в півплощину.

Решение упражнений

1. 1. Даны два отрезка АВ = 3 см и CD = 3,1 см. Существует перемещение, которое отображает отрезок АВ на CD? Почему?
2. 2. Треугольник ABC равносторонний. Существует перемещение, которое отражает:

а) отрезок АВ на ВС; б) угол В угол С?

1. 3. Докажите, что при перемещении углы между лучами сохраняются.

III. Закрепление и осмысление нового материала

Решение задач

1. 1. Докажите, что при перемещении подобные треугольники переходят в подобные треугольники.
2. 2. Докажите, что вследствие перемещения параллельные прямые переходят в параллельные прямые.

IV. Домашнее задание

1. 1. Изучить определение и свойства перемещения.
2. 2. Решить задачу.

Доказать, что при перемещении параллелограмм переходит в параллелограмм.

V. Подведение итогов урока

Вопрос к ученикам

1. 1. Дайте определение перемещения.
2. 2. Назовите свойства перемещения.
3. 3. Связь перемещения имеет с равенством фигур?