УРОК № 35

Тема. Симметрия относительно прямой

Цель урока: формирование понятия симметрии относительно прямой; изучение свойств симметрии относительно прямой; формирование умений применять изученные определения и свойства к решению задач.

Тип урока: комбинированный.

Наглядность и оборудование: таблица «Преобразование фигур. Движения» [13].

Требования к уровню подготовки учащихся: описывают симметрию относительно прямой; строит фигуры, в которые переходят данные фигуры при симметрии относительно прямой; приводят примеры фигур, имеющих ось симметрии; применяют изученные определения и свойства к решению задач.

Ход урока

И. Проверка домашнего задания

1. 1. Проверить наличие выполненных домашних заданий и ответить на вопросы, которые возникли у учащихся при их выполнении.
2. 2. Фронтальная беседа
3. 1) Дайте определение симметрии относительно точки.
4. 2) Какие фигуры называются центральносиметричними? Приведите примеры.
5. 3) Укажите координаты точки, которая симметрична точке A(a; b) относительно начала координат.

II. Поэтапное восприятие и осознание нового материала

Понятие симметрии относительно прямой

Точки X и X1 называются симметричными относительно прямой l, если прямая l является серединным перпендикуляром к отрезка ХХ1 (рис. 163), то есть если ОХ = ОХ1 и l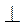XX1.

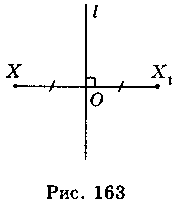
Преобразование фигуры F в фигуру F1, при котором каждая точка X фигуры F переходит в точку Х1 фигуры F1, симметричную ей относительно данной прямой l, называется преобразованием симметрии относительно прямой l или осевой симметрией (рис. 164). При этом фигуры F и F1 называются симметричными относительно прямой l, а прямая l - осью симметрии.

Свойства осевой симметрии

1. 1) Преобразование осевой симметрии является перемещением.
2. 2) Осевая симметрия превращает прямую на прямую; отрезок - отрезок; многоугольник - на равный ему многоугольник.
3. 3) Точки, принадлежащие оси симметрии, отображаются сами на себя.
4. 4) Если точки М(х; у) и N(x1; y1) симметричные (рис. 165) в отношении:

а) оси Ох, то выполняется условие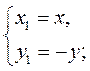

б) оси Оу, то выполняется условие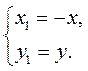

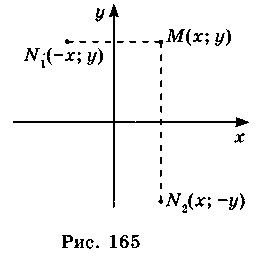
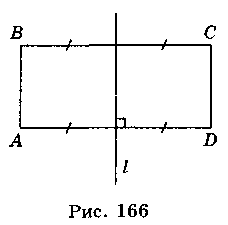
Если преобразование симметрии относительно прямой l переводит фигуру F в себя, то эта фигура называется симметричной относительно прямой l, а прямая l называется осью симметрии (рис. 166).

Выполнение упражнений

1. 1. Постройте произвольный треугольник ABC и симметричный ему треугольник относительно оси:

а) АВ; б) ВС.

1. 2. Сколько осей симметрии имеет:

а) круг;

б) прямоугольник;

в) квадрат;

г) ромб;

д) равносторонний треугольник?

III. Закрепление и осмысление нового материала

Решение задач

1. 1. Постройте произвольный треугольник и треугольник, симметричный данному, относительно прямой, если она:

а) расположена вне треугольника;

б) имеет только одну общую точку с треугольником;

в) пересекает две стороны треугольника.

1. 2. Четырехугольник ABCD задан координатами своих вершин: А(1; 1); В(-3; 2), С(-1; -2), D(5; -3). Найдите координаты вершин четырехугольника, симметричный данному относительно оси:

а) Х; б) Оу.

1. 3. Докажите свойства симметрии относительно прямой.
2. 4. Запишите уравнение окружности, которое симметричное окружности (х - 1)2 + (у + 2)2 = 1 в отношении:

а) оси Ох; б) оси Оу.

1. 5. Запишите уравнение прямой, которая симметрична прямой х + у = 1 в отношении:

а) оси Ох; б) оси Оу.

1. 6. Дано прямую MN и точки А и В в разных півплощинах относительно MN и на разном расстоянии от нее. Через точки А и В проведите прямые так, чтобы угол между ними делился прямой MN пополам.

IV. Домашнее задание

1. 1. Изучить теоретический материал.
2. 2. Решить задачи.
3. 1) Запишите уравнение окружности, которое симметричное окружности (х + 1)2 + (у + 1)2 = 1 в отношении:

а) оси Ох; б) оси Оу.

1. 2) Запишите уравнение прямой, которая симметрична прямой х - у = 1 в отношении:

а) оси Ох; б) оси Оу.

V. Подведение итогов урока

Вопрос к классу

1. 1. Какие точки называются симметричными относительно прямой?
2. 2. Какое преобразование называется симметрией относительно данной прямой?
3. 3. Какая фигура называется симметричной относительно данной прямой?
4. 4. Что такое ось симметрии? Приведите примеры.