Урок 34
Тема. Тематическое оценивание № 3
Цель урока: проверка знаний учащихся по темам «Перпендикулярность прямых», «Перпендикулярность прямой и плоскости».
Ход урока
Тематическое оценивание № 3 можно провести в виде тематической контрольной работы.
1. Тематическая контрольная работа № 3
Вариант А
Вариант 1
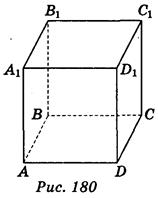
1. Пользуясь изображением куба ABCDA1B1C1D1 (рис. 180), запишите ребра куба, перпендикулярные к ребру АА1 и пересекают его. (3 балла)
2. Расстояние от точки М до всех вершин квадрата равна 10 см. Найти расстояние от точки М до плоскости квадрата, если диагональ квадрата равна 12 см. (3 балла)
3. Из точки А, взятой вне плоскости α, проведены к ней две наклонные, длины которых равны 10 и 17 см. Разность проекций этих наклонных на плоскость α равен 9 см. Найти проекции наклонных. (3 балла)
4. Правильный треугольник расположен над плоскостью. Докажите, что расстояние от центра треугольника до данной плоскости равен среднему арифметическому расстояний от вершин этого треугольника до этой плоскости. (3 балла)
Вариант 2
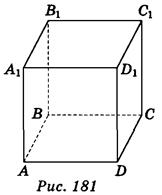
1. Пользуясь изображением куба ABCDA1B1С1D1 (рис. 181), запишите ребра, перпендикулярные грани ABCD. (3 балла)
2. Расстояния от точки М до всех вершин квадрата равны по 13 см, а к плоскости квадрата - 12 см. Найдите диагональ квадрата. (3 балла).
3. Из точки А, взятой вне плоскости α, проведены к ней две наклонные. Найдите длины наклонной, если одна из них на 13 см больше другой, а проекции наклонных на плоскость α равны 6 и 20 см. (3 балла)
4. Параллелограмм расположен над плоскостью. Докажите, что сумма расстояний от противоположных вершин параллелограмма до данной плоскости одинакова. (3 балла)
Вариант 3
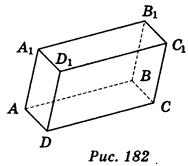
1. Пользуясь изображением прямоугольного параллелепипеда ABCDA1B1C1D1 (рис. 182), запишите грани, перпендикулярные к ребру АА1. (3 балла)
2. Расстояния от точки S до всех вершин правильного треугольника равны по 5 см, а к плоскости треугольника - 3 см. Найдите высоту треугольника. (3 балла)
3. Из некоторой точки проведены к данной плоскости две наклонные. Найти длины наклонных, если проекции наклонных равны 2 и 14 см, а наклонные относятся как 1 : 2. (3 балла)
4. Квадрат расположен над плоскостью. Докажите, что расстояние от центра квадрата до плоскости в четыре раза меньше суммы расстояний от вершин квадрата до плоскости. (3 балла)
Вариант 4
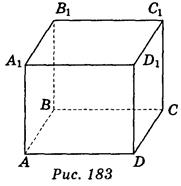
1. Пользуясь изображением прямоугольного параллелепипеда ABCDA1В1C1D1 (рис. 183), запишите ребра, перпендикулярные к ребру DC и пересекают его. (3 балла)
2. Расстояние от точки М до каждой вершины правильного треугольника равна 10 см. Найти расстояние от точки М до плоскости треугольника, если медиана треугольника равна 9 см. (3 балла)
3. Из некоторой точки пространства проведены две наклонные, проекции которых равны 8 и 20 см. Найти длины наклонных, если известно, что их разность равна 8 см. (3 балла)
4. Через вершину D параллелограмма ABCD проведена плоскость, которая пересекает его. Докажите, что расстояние от точки В до плоскости равен сумме расстояний от точек А и С до данной плоскости. (3 балла)
Ответ. Вариант 1. 1. А1В1, A1D1, AB, AD. 2. 8 см. 3. 6 см и 15 см.
Вариант 2. 1. АА1, ВВ1, СС1, DD1 2. 10 см. 3. 7,5 см и 20,5 .см. Вариант 3. 1. ABCD, A1B1D1. 2. 6 см. 3. 8 см и 16 см. Вариант 4. 1. DD1, DA, BC, CC1. 2. 8см. 3. 25 см и 17см.
Вариант Б
Вариант 1
1. Через центр О правильного треугольника АВС проведен перпендикуляр SO к плоскости АВС.
а) Какова величина угла SOA? (2 балла)
б) Докажите, что SA = SB. (2 балла)
в) Найдите расстояние от точки S до плоскости ABC, если SC = 5 см, 0В = 3 см. (2 балла)
2. Сторона квадрата ABCD равна 8 см. Точка S находится на расстоянии 16 см от его вершин. Найдите расстояние от точки S до плоскости квадрата. (3 балла)
3. В прямоугольном параллелепипеде АВСDА1В1С1D1 АВ1 = 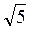 см, АС1 =
см, АС1 = 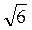 см, АВ = 2 см. Найдите расстояние между прямой A1D1 и плоскостью АВ1С1. (3 балла)
см, АВ = 2 см. Найдите расстояние между прямой A1D1 и плоскостью АВ1С1. (3 балла)
Вариант 2
1. Через центр О квадрата ABCD проведен перпендикуляр SO к плоскости АВС.
а) Какова величина угла SOD? (2 балла)
б) Докажите, что  SAO =
SAO =  SCO. (2 балла)
SCO. (2 балла)
в) Найдите расстояние SC, если расстояние от точки S до плоскости АВС равна 5 см, a OD = 12 см. (2 балла)
2. Точка S находится на расстоянии 6 см от вершин прямоугольника и на расстоянии 4 см от его плоскости. Найдите стороны прямоугольника, если одна из них вдвое больше второй. (3 балла)
3. Три отрезки SA, SB, SC имеют одинаковую длину а,  ASB=
ASB=  BSC =
BSC =  CSA = 60°. Найдите расстояние от точки S до плоскости АВС. (3 балла)
CSA = 60°. Найдите расстояние от точки S до плоскости АВС. (3 балла)
Вариант 3
1. Через центр О правильного шестиугольника ABCDEF проведена перпендикуляр SO к плоскости АВС.
а) Чему равен угол между прямыми SO и AD? (2 балла)
б) Докажите, что  ASO =
ASO =  FSO. (2 балла)
FSO. (2 балла)
в) Найдите сторону шестиугольника, если расстояние от точки S до плоскости АВС равно 4 см, а SC = 5 см. (2 балла)
2. Сторона правильного треугольника АВС равна 12 см. Точка S находится на одинаковом расстоянии от его вершин и удалена от плоскости треугольника на расстояние 4 см. Найдите расстояние от точки S до вершин треугольника АВС. (3 балла)
3. Ребро куба ABCDA1B1C1D1 равно а. Найдите расстояние от точки А до плоскости AB1D1. (3 балла)
Вариант 4
1. Через точку О пересечения диагоналей АС и BD прямоугольника ABCD проведен перпендикуляр SO к плоскости АВС.
а) Чему равен угол между прямыми SO и АС? (2 балла)
б) Докажите, что SA = SC. (2 балла)
в) Найдите расстояние от точки S до плоскости ABC, если SC = 10 см, OD = 6 см. (2 балла)
2. Точка S находится на расстоянии 10 см от вершин равнобедренного треугольника АВС (АВ = ВС) и на расстоянии 6 см от его плоскости. Найдите стороны треугольника, если  ВАС = 30°. (3 балла)
ВАС = 30°. (3 балла)
3. Три отрезки SA, SB, SC попарно перпендикулярны, SA = SB = SC = а. Найдите расстояние от точки S до плоскости АВС. (3 балла)
Тематическое оценивание № 3 можно провести с помощью теста, текст которого представлен ниже.
При оценивании выполнения тестов учитываются только те шесть из выполненных заданий, которым соответствует наибольшее количество баллов.
Тест
Перпендикулярность прямой и плоскости
Цель данного теста - проверить, умеет ли учащийся:
- изображать и находить на рисунке перпендикулярные прямые и плоскости;
- решать задачи, используя признак перпендикулярности прямой и плоскости.
Вариант 1
И уровень
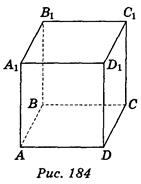
1. Дано изображение куба АВСDА1В1С1D1 (рис. 184). Укажите прямую, которая перпендикулярна к прямой АА, и проходит через точку С. (1 балл)
а) АВ; б) АС; в) AD; г) АС.
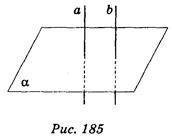
2. Известно, что различные прямые а и b перпендикулярны к плоскости α (рис. 185). Как расположены прямые а и b? (1 балл)
а) Пересекаются; б) скрещивающиеся; в) параллельны; г) перпендикулярны.
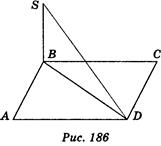
3. Отрезок SB перпендикулярен к плоскости прямоугольника ABCD (рис. 186). Найдите расстояние между точками S и D, если SB = 4 см, BD = 3 cm. (1 балл)
а) 3 см; б) 4 см; в) 5 cm; r) 7 cm.
II уровень
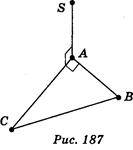
1. Точка S лежит вне плоскости треугольника АВС, причем  SAC = 90°,
SAC = 90°,  CAB = 90° (рис. 187). Какие из указанных утверждений верны? (1 балл)
CAB = 90° (рис. 187). Какие из указанных утверждений верны? (1 балл)
а) Прямая SA перпендикулярна к плоскости АВС;
б) прямая АВ перпендикулярна к плоскости SAC;
в) прямая АС перпендикулярна к плоскости SAB;
г) прямая ВС перпендикулярна к плоскости ASC.
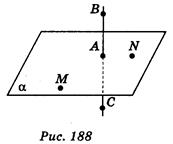
2. Точки А, В, С лежат на прямой, перпендикулярной к плоскости а , а точки А, М, N лежат в плоскости а (рис. 188). Какие из указанных углов прямые? (1 балл)
a)  MAB; б)
MAB; б)  MCA; в)
MCA; в)  CAN ; г)
CAN ; г)  NBA.
NBA.
3. В пространстве даны прямая а и точка А вне ее. Сколько существует прямых, перпендикулярных к прямой а и проходящих через точку А? (1 балл)
а) Никакой; б) множество; в) одна; г) определить невозможно.
III уровень
1. Прямые АВ и CD перпендикулярны некоторой плоскости и пересекают ее в точках В и D соответственно. Найдите АС, если АВ = 9 см, CD = 15 см, BD = 8 см и отрезок АС не пересекает данной плоскости. (2 балла)
а) 8 см; б) 9 см; в) 10 см; г) 15 см.
2. Через вершину В квадрата ABCD проведена прямая BS, перпендикулярную его плоскости. Какие из приведенных утверждений верны? (2 балла)
а) Прямая SD перпендикулярна к плоскости АВС;
б) прямая AD перпендикулярна к плоскости ASB;
в) прямая CD перпендикулярна к плоскости BSC;
г) прямая BD перпендикулярна к плоскости SBC.
3. Через точку О пересечения диагоналей прямоугольника ABCD проведен перпендикуляр МО. Найдите МО, если АВ = 6 см, ВС = 8 см, МА = 13 см. (2 балла)
а) 10 см; б) 11 см; в) 12 см; г) определить невозможно.
IV уровень
1. Дан параллелограмм ABCD и плоскость α, которая его не пересекает. Через вершины параллелограмма проведены прямые, перпендикулярные плоскости и пересекающие плоскость соответственно в точках А1, В1, С1, D1. Найдите длину отрезка DD1, если АА1 = 3 см, ВВ1 = 4 см, СС1 =5 см. (3 балла)
а) 2 см; б) 3 см; в) 4 см; г) 5 см.
2. Прямые АВ, АС и AD попарно перпендикулярны. Найти площадь треугольника BCD, если АВ = 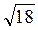 см, АС =
см, АС = 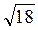 см, AD =
см, AD = 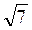 см. (3 балла)
см. (3 балла)
а) 25 см2; б) 16 см2; в) 15 см2; г) 12 см2.
3. Построено сечение куба ABCDA1В1C1D1 плоскостью, проходящей через точки В1 и D1 и середину ребра CD. Найдите периметр сечения, если ребро куба равно а. (3 балла)
a) 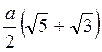 ; б)
; б) 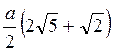 ; в)
; в) 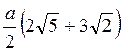 ; г)
; г) 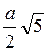 .
.
Вариант 2
И уровень
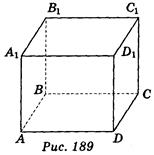
1. Дано изображение прямоугольного параллелепипеда АВСDА1В1С1D1 (рис. 189). Укажите плоскость, которая перпендикулярна к прямой AA1 и проходит через точку А. (1 балл)
a) DCC1; б) А1B1С1; в) BCD; г) ВСС1.
2. Как расположены плоскость α и прямая b, если a α, а || b (рис. 190)? (1 балл)
α, а || b (рис. 190)? (1 балл)
а) Не пересекаются;
б) параллельны;
в) перпендикулярны;
г) определить невозможно.
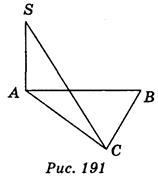
3. Отрезок SA перпендикулярен к плоскости треугольника АВС (рис. 191). Найдите расстояние от точки А до точки С, если SA = 3 см, SC = 5 см. (1 балл)
а) 3 см; б) 4 см; в) 5 см; г) 6 см.
II уровень
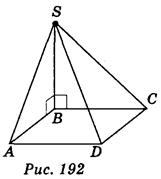
1. Точка S лежит вне плоскости ромба ABCD, причем SB BC, SB
BC, SB AS.
AS.  BAD = 30° (рис. 192). Какие из указанных утверждений верны? (1 балл)
BAD = 30° (рис. 192). Какие из указанных утверждений верны? (1 балл)
а) Прямая SB перпендикулярна к плоскости ADC;
б) прямая АВ перпендикулярна к плоскости SBC;
в) прямая BC перпендикулярна к плоскости ABS;
г) прямая SB перпендикулярна прямой BD.
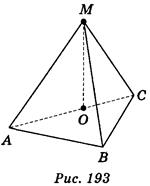
2.  ABC=90°, точка М лежит вне плоскости АВС, МА = МВ = МС. Из точки М проведен отрезок ОМ, который перпендикулярен к плоскости АВС, точка О лежит в плоскости АВС (рис. 193). Какие из указанных утверждений верны? (1 балл)
ABC=90°, точка М лежит вне плоскости АВС, МА = МВ = МС. Из точки М проведен отрезок ОМ, который перпендикулярен к плоскости АВС, точка О лежит в плоскости АВС (рис. 193). Какие из указанных утверждений верны? (1 балл)
а) Точка О лежит внутри треугольника АВС;
б) точка О лежит вне треугольника АВС;
в) точка О лежит на отрезке АС, причем АО не равен ОС;
г) точка О лежит на гипотенузе АС, причем АО равен ОС.
3. В пространстве даны прямая а и точка А на ней. Сколько существует прямых, перпендикулярных к прямой а, которые проходят через точку А? (1 балл)
а) Никакой; б) множество; в) только одна; г) определить невозможно.
III уровень
1. Прямые АВ и CD перпендикулярны некоторой плоскости и пересекают ее в точках соответственно. Найдите BD, если АВ = 6 см, CD = 9 см, AC = 5 см и отрезок АС не пересекает данной плоскости. (2 балла)
а) 1 см; б) 2 см; в) 3 см; г) 4 см.
2. Через точку О пересечения диагоналей прямоугольника ABCD проведен перпендикуляр МО к плоскости АВС. Какие из приведенных утверждений верны? (2 балла)
а) Прямая МО перпендикулярна к прямой АС;
б) прямая МО перпендикулярна плоскости BCD;
в) прямая AC перпендикулярна к плоскости ИМЕЛ;
г) прямая АС обязательно перпендикулярна к плоскости MBD.
3. Через вершину В квадрата ABCD проведена прямая BS, перпендикулярную его плоскости. Найдите расстояние от точки S до вершины А квадрата ABCD, если АС = 2 cm, SB = 1 cm. (2 балла)
а)  см; б) 1 см; в)
см; б) 1 см; в)  см; г) 2 cm.
см; г) 2 cm.
IV уровень
1. Точка О - точка пересечения медиан треугольника АВС, α - плоскость, которая не пересекает треугольник АВС. Через точки А, В, С, В проведены прямые, перпендикулярные к плоскости α, пересекающие плоскость соответственно в точках А1, В1, С1, В1. Найдите длину отрезка OO1, если АА1 = 1 см, ВВ1 = 2 см, СС1 = 3 см. (3 балла)
а) 1 см; б) 2 см; в) 3 см; г) 1,5 см.
2. Дан прямоугольный параллелепипед ABCDA1B1C1D1, в котором BD = 13 см, DC = 5 см, СС1 = 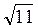 см. Найдите площадь треугольника ADC1. (3 балла)
см. Найдите площадь треугольника ADC1. (3 балла)
а) 25 см2; б) 36 см2; в) 72 см2; г) 18 см2,
3. В кубе ABCDA1B1C1D1 построено сечение плоскостью, проходящей через точки А, С, К, где К - середина ребра C1D1. Найдите периметр сечения, если ребро куба равно а. (3 балла)
а) 2а; б) 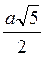 ; в)
; в) 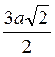 ; г)
; г) 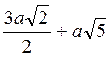 .
.
Ответы к тестовым заданиям
Уровень |
Номер задания |
Вариант 1 |
Вариант 2 |
И |
1 |
б |
в |
2 |
в |
в |
3 |
в |
б |
II |
1 |
в |
а, г |
2 |
а, в |
г |
3 |
в |
б |
III |
1 |
в |
г |
2 |
б, в |
а, б |
3 |
в |
в |
IV |
1 |
в |
б |
2 |
г |
б |
3 |
в |
г |
II. Домашнее задание
Если в классе выполнялась тематическая контрольная работа № 3, то дома можно предложить выполнить тест, и наоборот.
III. Подведение итога урока
В ходе фронтальной беседы выяснить, какие задания вызвали трудности, и ответить на вопросы учеников.









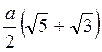 ; б)
; б) 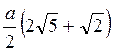 ; в)
; в) 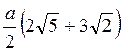 ; г)
; г) 




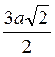 ; г)
; г) 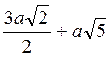 .
.