Урок 33
Тема. Решение задач
Цель урока: формирование умений учащихся применять свойства точки, равноудаленной от вершин многоугольника, и знаний о расстояние от прямой до параллельной ей плоскости, расстояние между параллельными плоскостями к решению задач.
Оборудование: стереометрический набор.
Ход урока
И. Проверка домашнего задания.
1. Два ученика воспроизводят решения задач № 17, 19 на доске.
2. Математический диктант.
Из центра правильного:
вариант 1 - треугольника (рис. 175);
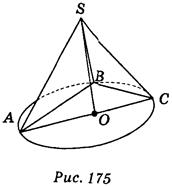
вариант 2 - четырехугольника (рис. 176) проведен перпендикуляр SO к плоскости АВС, SO = 1 см, АВ = 1 см.
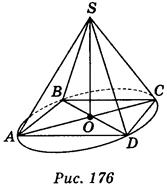
Пользуясь рисунком, найдите:
1) проекцию наклонной SA на плоскость АВС; (2 балла)
2) отрезки, равные отрезку ОА; (2 балла)
3) наклонные, равные наклонной SA; (2 балла)
4) длину наклонной SA; (2 балла)
5) угол между наклонной SA и перпендикуляром SO; (2 балла)
6) высоту треугольника SAB, проведенную из вершины S. (2 балла)
Ответ.
Вариант 1. 1) 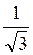 см; 2) 0В, ОС; 3) SB, SC; 4)
см; 2) 0В, ОС; 3) SB, SC; 4) 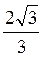 см; 5) arctg
см; 5) arctg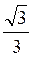 =300; 6)
=300; 6) 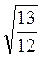 см.
см.
Вариант 2. 1)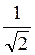 см; 2) OB, ОС, OD; 3) SB, SC, SD; 4)
см; 2) OB, ОС, OD; 3) SB, SC, SD; 4)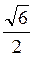 см; 5) arctg
см; 5) arctg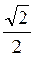 ; 6)
; 6) 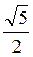 см.
см.
3. Обсуждение правильности выполнения учащимися задач на доске.
II. Закрепление и осмысление знаний учащихся
Решение задач
1. В рівнобедреному треугольнике угол при вершине равен 120°, а боковые стороны по 10 см. Вне плоскости треугольника дана точка, удаленная от каждой из вершин на 26 см. Найдите расстояние от этой точки до плоскости треугольника. (Ответ. 24 см.)
2. В треугольнике АВС  А = 45°, ВС = 12 см. Точка S находится от его плоскости на расстоянии 6 см и на одинаковом расстоянии от каждой вершины треугольника. Найдите расстояние от точки S до вершин треугольника. (Ответ. 6
А = 45°, ВС = 12 см. Точка S находится от его плоскости на расстоянии 6 см и на одинаковом расстоянии от каждой вершины треугольника. Найдите расстояние от точки S до вершин треугольника. (Ответ. 6 см.)
см.)
3. Трапеция вписана в окружность, причем меньшая основа, которая равна 16 см, стягивает дугу в 60°. На расстоянии 12 см от плоскости трапеции находится точка, равноудаленная от каждой ее вершины. Найдите расстояние от этой точки до вершины трапеции. (Ответ. 20 см.)
III. Восприятие и осознание нового материала
Понятие расстояния от прямой до параллельной ей плоскости
Расстоянием от прямой до параллельной ей плоскости называется расстояние от любой точки этой прямой до плоскости.
Решение задач.
1. Задача № 26 из учебника (с. 36).
2. Задача № 28 из учебника (с. 36).
Решение
Пусть ABCD - ромб; ВВ1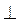 α; СС1
α; СС1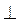 α; AD
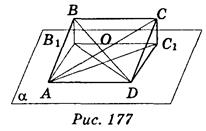
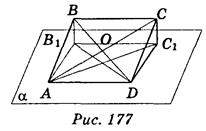
α; AD 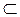 α; ВВ1 = СС1 = 4 м, B1D = 2 м, АС1 = 8 м (рис. 177). Поскольку AD || ВС; ВС || В1C1; AD = ВС = В1С1, то AB1C1D - параллелограмм.
α; ВВ1 = СС1 = 4 м, B1D = 2 м, АС1 = 8 м (рис. 177). Поскольку AD || ВС; ВС || В1C1; AD = ВС = В1С1, то AB1C1D - параллелограмм.
С ΔВВ1D: BD = 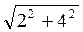 =
= 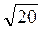 = 2
= 2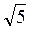 (см).
(см).
Из ΔАСС1: АС = 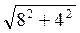 =
= 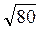 = 4
= 4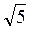 (см).
(см).
Из ΔАОВ: АВ = 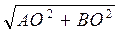 =
= 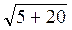 =
= 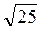 = 5 (см).
= 5 (см).
Из ΔАВВ1: АВ1 = 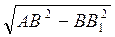 =
= 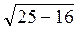 =
= 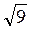 = 3 (см).
= 3 (см).
Відповідь.3 см и 5 см.
Понятие расстояния между параллельными плоскостями
Расстоянием между параллельными, плоскостями называется расстояние от любой точки одной плоскости до другой плоскости.
Решение задач
1. Задача № 30 из учебника (с. 36).
2. Задача № 32 из учебника (с. 36).
Решение
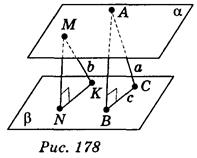
Пусть α || β; 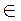 α М
α М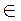 α С
α С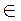 β, K
β, K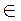 β; АВ
β; АВ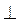 β; MN
β; MN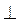 β; АС = а, МК = b, ВС = с (рис. 178).
β; АС = а, МК = b, ВС = с (рис. 178).
Из ΔАВС AB =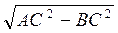 =
= 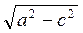 . Поскольку АВ = MN, то с ΔMNK: NK =
. Поскольку АВ = MN, то с ΔMNK: NK =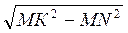 =
=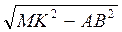 =
= 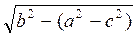 =
= 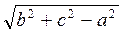 .
.
Ответ.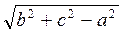 .
.
IV. Домашнее задание
Подготовиться к тематической аттестации № 3 решить задачи № 27, 31 (с. 36).
V. Подведение итога урока
Вопрос к классу
1) Что понимают под расстоянием между прямой и параллельной ей плоскостью?
2) Найдите расстояние от прямой а до плоскости АВС, если ребро куба равно 6 см (рис. 179).
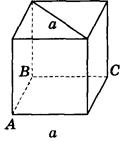
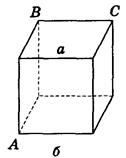
Рис. 179
3) Что называется расстоянием между параллельными плоскостями?
4) Дано изображение куба ABCDА1B1С1D1. Ребро куба равно 10 см. Найдите расстояние между плоскостями: а) АВС и А1В1С1; б) А1АВ и D1DC.