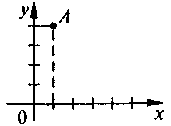|
2. Функция задана формулой у = х2. Найдите значение у, если х = -2
3. Какое утверждение является неправильным?
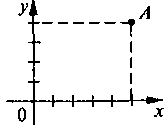
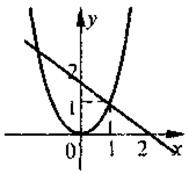
4. Определите уравнение, решение которого изображен на рисунке?
III. Формулировка цели и задач урока С целью создания проблемной ситуации и соответствующей мотивации деятельности учащихся можно предложить задание: Решить уравнение вида x + a = b, ax = b (относительно переменной х) и ответить на вопрос о способе вычисления корней них рівнянь. х2 = а (если такие существуют) для различных значений переменной (параметра). Далее учитель предлагает (ссылаясь на знания учащихся по количеству и существование корней уравнения х2 = а, приобретенные на предыдущем уроке) решить уравнение вида х2 = а и ответить на вопрос о действие, которое следует выполнить для отыскания корней названного уравнения. Осознание проблемы, что при этом возникает (ученикам пока неизвестна действие, с помощью которой можно найти число, квадрат которого известен), позволяет учителю при участии учащихся сформулировать цель урока: ознакомление учащихся с новым действием, что поможет найти число по значению его квадрата (изучение обозначения этого действия и особенностей ее выполнения).
IV. Актуализация опорных знаний и умений @ С целью успешного восприятия учащимися учебного материала урока перед изучением нового материала следует активизировать знания и умения учащихся: возведение рациональных чисел в квадрат; применение свойства степени с четным показателем; применение свойств функции у = х2 и ее свойств графика; содержание понятия ОДЗ выражения и способы нахождения ОДЗ рациональных выражений.
Выполнение устных упражнений 1. Поднесите ко второму степени числа: 0; 2; -2; 0,3; 2. Квадраты каких чисел равны: 0; 1; -0,2; 3. Точка А(k; 6) принадлежит графику функции у = х2. Принадлежит ли этому графику точки: В(k; -6); С(k; 6); Г(-k; -6)? Ответ обоснуйте. 4. Найдите ОДЗ выражения: 3х + 2;
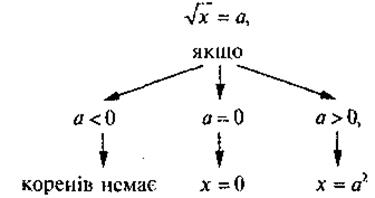
V. Усвоение знаний План изучения нового материала 1. Представление о квадратный корень из неотъемлемого числа как корень уравнения х2 = а. 2. Определение арифметического квадратного корня из неотъемлемого числа. ОДЗ выражения 3. Как вычислить значение арифметического квадратного корня из неотъемлемого числа. 4. Как решить уравнение
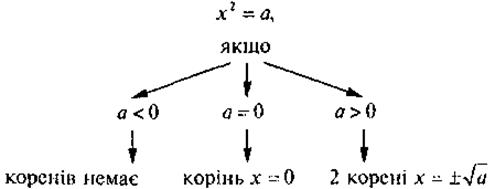
@ Традиционно формирование представления учащихся о содержании действия извлечения квадратного корня проводится на примере решения задачи на нахождение корней уравнения х2 = а, где а - некоторое число (желательно для возможности сравнения рассмотреть несколько примеров, различных по знаку значений а, используя при этом представление учащихся о свойствах графика функции у = х2). Тогда квадратными корнями называют именно корни уравнения х2 = а (а > 0). После чего следует заметить, что в случае, когда уравнение масс два корня, задача о нахождении квадратного корня из положительного числа решается неоднозначно, а это означает, то существует необходимость в определенной способа уточнения, о какой именно квадратный корень из положительного числа идет речь в задаче. Таким образом объясняется необходимость введения понятия арифметического квадратного корня из числа. Определение арифметического квадратной корня из неотъемлемого числа формулируется как в словесном виде (см. опорный конспект), так и в традиционной форме тождества. Обсуждая сформулированное определение, следует еще раз подчеркнуть, что операция извлечения квадратного корня из числа выполняется только для неотрицательных чисел (ОДЗ выражения По определению арифметического квадратного корня из неотъемлемого числа тесно связана схема решения уравнения Важно, чтобы ученики осознали разницу в понятиях квадратного корня и арифметического квадратного корня (как в форме записи, так и в определениях). Этому будет способствовать большое количество решенных на уроке и дома разноплановых задач.
VI. Формирование умений Выполнение устных упражнений 1. Найдите все квадратные корни из чисел; арифметический квадратный корень из чисел: а) 49; б) 1; в) 0; г) - 25. 2. Докажите, что: а) 3. Имеет ли смысл выражение: а) 4. Найдите квадраты чисел: 10; -8; 5. Найдите значения выражений при х = -5: х2; (х - 2)2; (х + 1)2; (х + 4)2; |х|; |х - 5|; 2|х| - 3; Выполнение письменных упражнений Традиционно для письменного решения на первом уроке изучения определение квадратного корня и арифметического квадратного корня предлагаются упражнения следующего содержания: 1. Доказательства, что данное число является (или не является) значением арифметического квадратного корня из данного числа. 1) Докажите, что: а) число 5 является арифметическим квадратным корнем из 25; б) число 0,3 является арифметическим квадратным корнем из 0,09; в) число - 7 не является арифметическим квадратным корнем из 49; г) число 0,6 не является арифметическим квадратным корнем из 3,6. 2) Докажите, что: а) 3) Докажите, что: а) 4) правильная Ли равенство: а) 5) Докажите, что: а) 2. Нахождение значения арифметического квадратного корня (выражения), содержащего арифметический квадратный корень. 1) Вычислите: а) 2) Вычислите: а) 3) Найдите значение выражения: а) 3. Определение масс содержание выражение, содержащее арифметический квадратный корень из числа. 1) имеет Ли смысл выражение: а) 2) При каких значениях х имеет смысл выражение: а) 3) имеет Ли смысл выражение: а) 4. Решение уравнений вида (или сводится к виду) 1) существует Ли значение переменной х, при котором: а) 2) Найдите значение переменной х, при котором правильное равенство: а) 5. Логические упражнения и задачи повышенного уровня сложности для учащихся, имеющих достаточный и высокий уровни знаний. 1) Решите уравнение: а) 5 2) Вставьте пропущенное число:
@ Упражнения, предлагаемые для решения на уроке, способствуют усвоению учащимися определений квадратного корня и арифметического квадратного корня (см. первый и второй вид задач), усвоению знаний о ОДЗ выражения
VII. Итоги урока В любом из случаев правильно выполнено действие? а)
VIII. Домашнее задание 1. Изучить определение квадратного корня и арифметического квадратного корня, содержание свойств и алгоритмов, изученных на уроке. 2. Решить упражнения на применение изученных понятий (по содержанию аналогичные задач классной работы). 3. Повторить: определение уравнения с одной переменной и содержание сопутствующих понятий; графики функций у = а и у = х2; решить задачи на построение графиков.
|
|
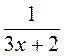 ;
; 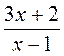 ;
; 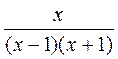
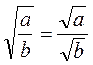 и наоборот
и наоборот 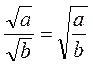
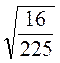 .
.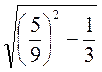 ?
?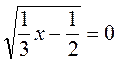 .
.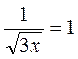 ; в)
; в) 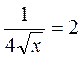 ; г)
; г)