Урок № 33
Тема. Задачи на деление дробей. Нахождение числа по его дроби
Цель: добиться усвоения учащимися алгоритма решения задач на нахождение числа по его дроби (процентами); повторить алгоритмы решения других задач на деление; вырабатывать умение решать задачи на применение названных алгоритмов.
Тип урока: усвоение знаний и умений.
Ход урока
И. Актуализация опорных знаний
Устные упражнения
1. Выполните деление: 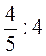 ;
; 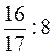 ;
; 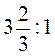 ;
; 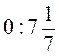 ;
; 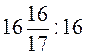 .
.
2. Решите уравнения: 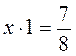 ;
; 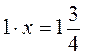 ;
; 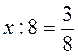 ;
; 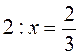 ;
; 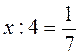 .
.
3. Отрезок длиной 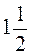 дм разделить на 3 равных части. Чему равна длина одной части?
дм разделить на 3 равных части. Чему равна длина одной части?
4. Найдите скорость пешехода, если путь в 5 км он преодолевает за 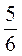 часа.
часа.
5. Данное число увеличили в 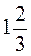 раза и получили
раза и получили 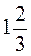 . Какое было число до увеличения?
. Какое было число до увеличения?
6. Как найти 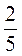 от 2000 м2? 40 % от 2000 м2?
от 2000 м2? 40 % от 2000 м2?
7. Выразите дробью (десятичным или обычным): 50 %; 3 %; 25 %; 37 %; 137%; 180%; 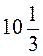 %.
%.
II. Систематизация знаний. Мотивация деятельности
@ После решения устных упражнений (№ 3, 4, 5) делаем вывод: с некоторыми видами задач на деление мы знакомы (1) задача на нахождение скорости движения по известным временем и расстоянием; 2) нахождение числа, которое меньше данного в 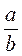 раз; 3) также задачи на нахождение доли от деления целого на несколько равных частей и др.); но есть еще один вид задач, которые решаются делением.
раз; 3) также задачи на нахождение доли от деления целого на несколько равных частей и др.); но есть еще один вид задач, которые решаются делением.
III. Усвоение знаний (фронтальная работа)
1. Задача. Расчистили от снега 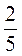 катка, что составляет 800 м2. Найдите площадь катка.
катка, что составляет 800 м2. Найдите площадь катка.
Решения. Пусть площадь катка х м2.
По условию 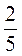 от х (г) равна 800 м2. (*)
от х (г) равна 800 м2. (*)
Итак, 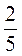 · х = 800, то есть х = 800 :
· х = 800, то есть х = 800 : 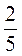 . (**); х = 800 ·
. (**); х = 800 · 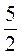 = 2000.
= 2000.
Ответ. Площадь катка 2000 м2.
Сравнив (*) и (**), делаем вывод:
Чтобы найти число по данному значению его дроби, надо это значение разделить на дробь.
@ Для «сильных» учеников этот материал можно записать в виде формулы.
Если 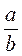 от х составляет с, х = с :
от х составляет с, х = с : 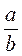 .
.
Пример
1. Задача. Рожью засеяно 2 400 га, что составляет 0,8 всего поля. Найдите площадь поля.
Решения. Поскольку известно, что 0,8 от (х) поля составляет 2 400 га, то х = 2400 : 0,8 = 3000 га.
2. Задача. Масса сушеной рыбы составляет 55 % массы свежей рыбы. Сколько надо взять свежей рыбы, чтобы получить 231 кг сушеной рыбы.
Решения. Понятно, что надо найти х, если 55 % от х составляет 231 кг.
Задача отличается от задачи в п.1 только величиной «55 %». Но же 55 % = 0,55, поэтому:
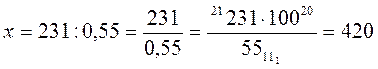 (кг).
(кг).
Вывод. Чтобы найти число по значению его процентов, надо:
1) записать проценты дробью;
2) разделить значение процентов на этот дробь.
Пример
Увеличив производительность труда на 7 %, рабочий выполнил за то же время на 98 деталей больше, чем было запланировано. Сколько деталей должен был изготовить рабочий по плану?
Решение. 7 % = 0,07; 98 : 0,07 = 1 400.
Ответ. По плану 1 400 деталей.
В тетрадях имеем запись в виде конспекта 21.
Конспект 21 |
Нахождение числа по значению его дроби (процентов) |
Правило 1) Найдите х, если 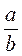 от х составляет с: х = с : от х составляет с: х = с : 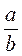 . .
2) Найдите х, если р % от х составляет с: а) г % выражаем в виде 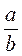 ; ;
б) х = с : 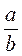 . . |
Пример
1) Найдите число, если 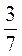 его 21. его 21.
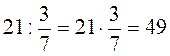 . .
2) Найдите число, если 30 % его составляет 90:
а) 30% = 0,3; б) 90 : 0,3 = 300. |
IV. Усвоение умений
@ Задачи такого типа, которые решаются на этом уроке, уже встречались учащимся (5 класс). Но, в отличие от изученного ранее способа, подобные задачи мы должны теперь научиться решать делением. Поэтому следует убедить учащихся в том, что разобран на уроке способ является лучшим, и требовать от учащихся находить число по его дроби (процентами) только делением!
И уровень
Устные упражнения
1. На приусадебном участке собрали 8 кг огурцов, что составляет 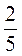 собранных овощей. Сколько килограммов овощей собрали?
собранных овощей. Сколько килограммов овощей собрали?
2. На приусадебном участке собрали 8 кг огурцов, что составляет 0,4 собранных овощей. Сколько килограммов овощей собрали?
3. На приусадебном участке собрали 8 кг огурцов, что составляет 40 % собранных овощей. Сколько килограммов овощей собрали?
II уровень
1. Какой путь пройдет группа туристов за 1 ч, если 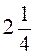 км она проходит за
км она проходит за 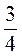 ч;
ч; 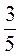 ч;
ч;  ч?
ч?
2. По 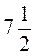 м ткани заплатить 183 грн 75 к. Какова цена одного метра ткани?
м ткани заплатить 183 грн 75 к. Какова цена одного метра ткани?
3. Длина земельного участка прямоугольной формы 40 м, а ширина - в 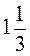 раза меньше. Найдите площадь участка.
раза меньше. Найдите площадь участка.
4. Одна сторона треугольника равна 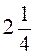 м, а вторая и третья - соответственно в
м, а вторая и третья - соответственно в 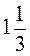 и
и 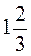 раза длиннее первой. Найдите периметр треугольника.
раза длиннее первой. Найдите периметр треугольника.
5. Найдите число: а) 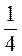 которого равна 21; б)
которого равна 21; б) 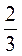 которого равен 30; в) 0,7 которого равна 14; г) 0,21 которого равна 0,609.
которого равен 30; в) 0,7 которого равна 14; г) 0,21 которого равна 0,609.
6. Кукурузой засеяли 78 га поля, что составляет 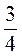 площади всего поля. Какова площадь всего поля?
площади всего поля. Какова площадь всего поля?
7. Найдите число: а) 15 % которого равен 36; б) 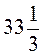 % которого равен 41.
% которого равен 41.
8. Из ржи получают 75% муки. Сколько пшеницы нужно смолоть, чтобы получить 60 кг муки?
9. Ширина пастбища прямоугольной формы 30 м, что составляет 48 % длины. Какова площадь пастбища? - Задачи на нахождение числа по его дроби (процентами).
Дополнительно (на повторение)
1. Найдите значение выражения:
а) 8,45 · 9,6 - 7,8 · 8,45;
б) 37,5 + (62,8 - 27,5): 4.
2. а) 31,2 : х + 6,7, если х = 10;
б) 38,5+ а : b, если а = 19,8, b = 90.
V. Итоги урока
Из выражений является решением задачи?
На линию вышло 56 автобусов, что составляет 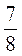 всех автобусов автопарка. Сколько автобусов в автопарке?
всех автобусов автопарка. Сколько автобусов в автопарке?
1) 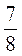 · 56; 2)
· 56; 2) 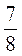 : 56; 3) 56 :
: 56; 3) 56 : 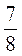 ; 4) 56 +
; 4) 56 + 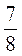 .
.
VI. Домашнее задание
1. Найдите число: а) 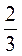 которого равен 25; б)
которого равен 25; б) 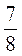 которого равен
которого равен 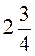 .
.
2. Автомат расфасовывает желатин в пакетики по 0,03 кг. Сколько пакетиков нужно для расфасовки 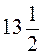 кг желатина?
кг желатина?
3. Велосипедист движется со скоростью 21 км/ч, что составляет 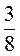 скорости автомобиля. Какова скорость автомобиля?
скорости автомобиля. Какова скорость автомобиля?
4. Найдите число: а) 35% которого равен 7; б) 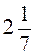 % которого равен 1,5.
% которого равен 1,5.
5. В классе три отличника, что составляет 12 % всех учащихся класса. Сколько учеников в классе?
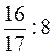 ;
; 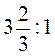 ;
; 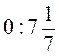 ;
; 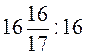 .
.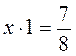 ;
; 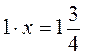 ;
; 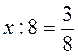 ;
; 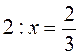 ;
; 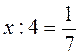 .
.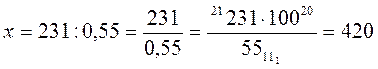 (кг).
(кг).