Урок № 32

Тема. Свойства углов, образованных при пересечении двух параллельных прямых секущей

Цель: закрепить знания учащихся о содержании и схему доказательства теоремы о свойстве углов и последствий с нее; сформировать представление учащихся о расстояние между двумя параллельными прямыми; сформировать умение использовать названные выше теоретические сведения при решение задач на нахождение углов при параллельных прямых и секущей и расстояния между параллельными прямыми.

Тип урока: применение знаний, умений и навыков.

Наглядность и оборудование: набор демонстрационного чертежных принадлежностей; таблица «Свойства углов...»

ХОД УРОКА

I. Организационный момент

II. Проверка домашнего задания

Домашнее задание проверяем по образцу взаимопроверкой.

III. Мотивация учебной деятельности. Формулировка цели и задач урока

Для создания положительной мотивации можно предложить учащимся к решению проблему (создать проблемную ситуацию).

Как найти расстояние от точки A до точки B?

Как найти расстояние от точки A до прямой b? При каком взаимном расположении A и b может идти речь расстояние между ними?

Как найти расстояние от прямой a до прямой b? При каком взаимном расположении a и b может идти речь расстояние между ними?

Последний вопрос и побуждает учеников к изучению вопроса, вынесенного в тему урока, и поиск ответа на него есть по сути основной целью урока.

IV. Актуализация опорных знаний

Выполнение устных упражнений

1. Найдите все неизвестные углы на рисунке 1, если a||b:

а)

б)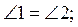

в)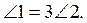

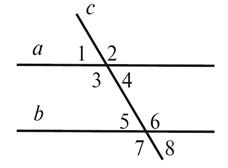
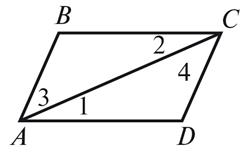
2. Дано: AB || CD, BC || AD (рис. 2).Доведіть,что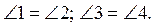

3. Укажите взаимное расположение прямых b и c, если a||b,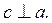

V. Усвоение новых знаний

План изучения нового материала

1°. Теорема о расстояния от точек прямой до параллельной прямой (с доводкой).

2°. Определение расстояния между параллельными прямыми. Понятия общего перпендикуляра к параллельным прямых.

Методический комментарий

В отличие от учебника О. В. Погорелова, в котором утверждение теоремы вынесено в опорную задачу (§ 4, № 50), учебник авторов А. П. Ершовой и др. содержит это именно утверждение в виде самостоятельной теоремы, что наверное свидетельствует о достаточно важное место этому вопросу. Также новый учебник содержит иной подход к доказательства (со ссылкой на следствие из теоремы о свойстве углов, образованных при пересечении параллельных прямых секущей). Учитель также может обратить внимание на уместно в этом месте понятия общего перпендикуляра к двум параллельным прямых.

VI. Первичное осознание нового материала

Выполнение устных упражнений

Один из углов, образованных в результате пересечения двух параллельных прямых секущей, равен 120°. Может ли один из остальных семи углов равняться 50°? Почему?

Выполнение письменных упражнений

1. Прямые a и b параллельны. Точки A₁ и A₂ лежат на прямой a, отрезки A₁B₁ и A₂B₂ -расстояния между прямыми a и b. Назовите отрезки, которые есть расстояниями между прямыми A₁B₁ и A₂B₂. Ответ обоснуйте.

2. Отрезок AB - расстояние между параллельными прямыми a и b. Точка M-середина отрезка AB. Докажите, что любой отрезок с концами на данных прямых, который проходит через точку M, делится ею пополам.

VII. Усвоение навыков

На уроке желательно уделить внимание решению задач на совместное применение признаков и свойств параллельных прямых. Целесообразно на уроке решить типовые для этой темы задачи.

Уровень Б

По данным рисунка 3 найдите угол x.

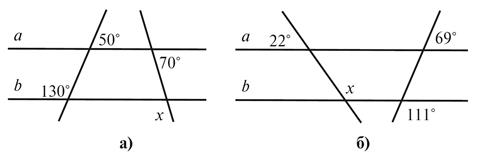
Уровень В

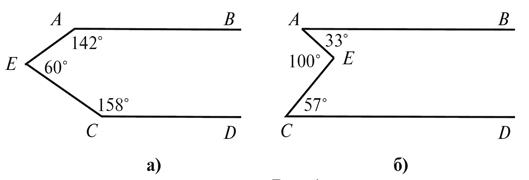
1. По данным рисунка 4, а, б определите, параллельные прямые AB и CD.

2. Биссектрисы внутренних односторонних углов, образованных в результате пересечения двух параллельных прямых секущей, взаимно перпендикулярны. Докажите.

3. Биссектрисы внутренних разносторонних углов, образованных в результате пересечения двух параллельных прямых секущей, параллельны. Докажите.

VIII. Итоги урока

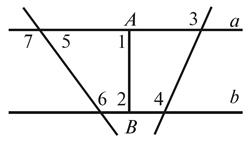
На рисунке 5 AB - расстояние между прямыми a и b. Что можно сказать об углы, обозначенные на рисунке 5?

IX. Домашнее задание

Изучить теоретический материал.

Решить задачи.

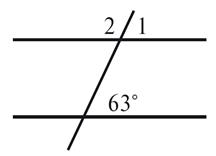
1. По данным рисунка 6, определите, параллельные прямые a и b, если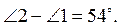

2. Через вершину B равнобедренного треугольника ABC проведена прямая l, параллельная основе AC. Отрезок BK - медиана треугольника ABC. Докажите, что BK - расстояние между прямыми l и AC.

3. Дано равнобедренный треугольник ABC с основанием AC. Прямая, параллельная AC, пересекает сторону AB в точке A₁ , а сторону BC - в точке C₁. Докажите, что треугольник A₁BC₁ равнобедренный.

Или ученикам можно предложить домашнюю самостоятельную работу.

Домашняя самостоятельная работа

Вариант 1

Начальный уровень

1. Разница двух с восьми углов, образовавшихся при пересечении двух параллельных прямых секущей, равен 54° . Найдите каждый из восьми углов.

Средний уровень

2. Секущая пересекает две данные прямые; при этом образовались внутренние односторонние углы, разность которых равен 108°, а отношение - 4 : 1. Докажите, что данные прямые параллельны.

Достаточный уровень

3. Отрезки AB и CD есть параллельными и ровными. Докажите, что Δ ABC = Δ DCB, если отрезки AD и BC пересекаются.

Высокий уровень

4. Через точки A и B, что лежат на сторонах тупого угла AOB, проведены прямые, параллельные сторонам данного угла и пересекающиеся в точке C. Найдите угол AOB, если прямые AC и BC пересекаются под углом 40°.

Вариант 2

Начальный уровень

1. Сумма двух из восьми углов, образовавшихся при пересечении двух параллельных прямых секущей, равен 72° . Найдите каждый из восьми углов.

Средний уровень

2. Секущая пересекает две данные прямые; при этом образовались внутренние односторонние углы, разность которых равен 36°, а отношение - 3 : 2. Докажите, что данные прямые параллельны.

Достаточный уровень

3. Отрезки AB и CD есть параллельными и ровными. Докажите, что Δ AOB = Δ DOC, где O - точка пересечения отрезков AD и BC.

Высокий уровень

4. Угол AOB равен 135°. Через точки A и B проведены прямые, параллельные сторонам данного угла и пересекаются в точке C. Под каким углом пересекаются эти прямые?

Источники:

1. Уроки геометрии. 7 класс./ С. П. Бабенко - Х.: Изд. группа «Основа», 2007.- 208 с.