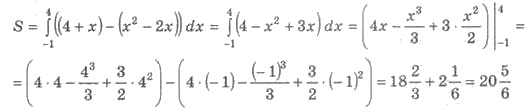АЛГЕБРА И НАЧАЛА АНАЛИЗА
Раздел III. ФУНКЦИЯ
§24. ПРИМЕНЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА К ВЫЧИСЛЕНИЮ ПЛОЩАДЕЙ КРИВОЛИНЕЙНЫХ ТРАПЕЦИЙ ПЛОЩАДЕЙ ПЛОСКИХ ФИГУР И ПРИКЛАДНЫХ ЗАДАЧ.
2. Вычисление площадей плоских фигур.
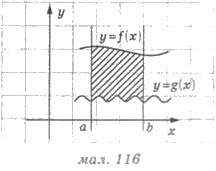
Рассмотрим площадь фигур сверху
ограниченную графиком функции у = /(х), снизу - графиком функции у = f(х) и вертикальными прямыми х = а и
х = b, причем функции у = f(x) и у = g(х) - непрерывные на [а;b] и для всех значений х 
[а;b] выполняется неравенство f(x) ≥ g(x) (рис. 116). Тогда площадь S такой плоской фигуры можно найти по формуле:
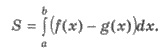
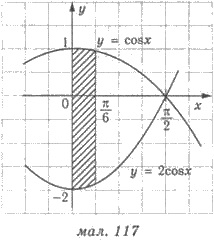
Пример 1. Найдите площадь фигур,
ограниченную графиками функций у = соs
х, у = -2 соs х и прямыми
x = 0 и x = π/6.
Решение (рис. 117). Имеем
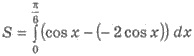
Підінтегральний выражение можно
упростить. Получим
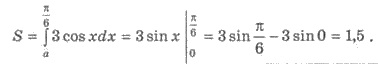
Пример 2. Найдите площадь фигуры,
ограниченную графиками функций у = х2 - 2х и у = 4х + х.
Решения. Найдем абсциссы точек
пересечения графиков функций:
х2 - 2х = 4
+ х; х2 - 3х - 4 = 0; x1 = -1; x2 = 4.
Ординаты точек пересечения y1 = 3; в2
= 8. Изображаем графики функций схематично (рис. 118).
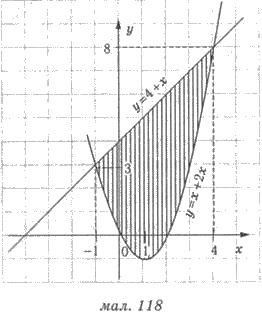
Искомая площадь
