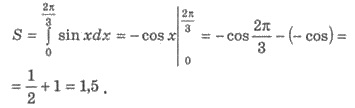АЛГЕБРА И НАЧАЛА АНАЛИЗА
Раздел III. ФУНКЦИЯ
§24. ПРИМЕНЕНИЕ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА К ВЫЧИСЛЕНИЮ ПЛОЩАДЕЙ КРИВОЛИНЕЙНЫХ ТРАПЕЦИЙ ПЛОЩАДЕЙ ПЛОСКИХ ФИГУР И ПРИКЛАДНЫХ ЗАДАЧ.
1. Определение криволинейной трапеции и нахождение ее площади.
Пусть на отрезке [а;b] оси абсцисс задана непрерывная
функцию у = f(x), которая на этом отрезке приобретает лишь только неотъемлемые
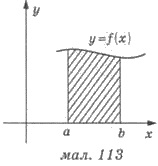
значение. Фигуру, ограниченную графиком функции у = =f(х), осью абсцисс и прямыми х = а, х = b , называют криволинейной трапецией
(рис. 113). Ее площадь S можно найти с помощью
определенного интеграла
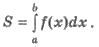
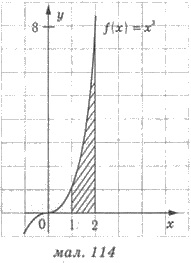
Пример 1. Вычислите площадь
криволинейной трапеции, исчисленной графику
функции f(х) = х3 и прямыми у =
0; х = 1; х = 2.
Решение (рис. 114). Имеем
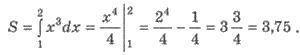
Пример 2. Вычислите площадь
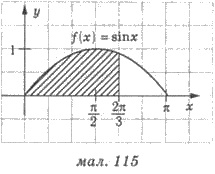
криволинейной трапеции ограниченной графиком функции f(x) = sin х и прямыми 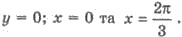
Решение (рис. 115). Имеем