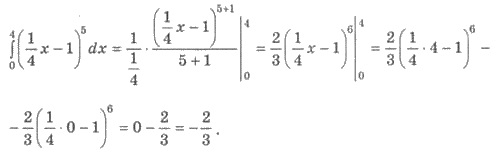АЛГЕБРА И НАЧАЛА АНАЛИЗА

Раздел III. ФУНКЦИЯ

§23. ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. ФОРМУЛА НЬЮТОНА-ЛЕЙБНИЦА.

Дадим одно из определений определенного интеграла.

Определенным интегралом от непрерывной на [а;b] функции f(x) с нижним пределом а и верхним пределом b называют разностью F(b) - F(a), где F(x) - одна из первичных для функции f(x). Обозначают определенный интеграл так 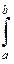f(x)dx.

При вычислении разности F(b) - F(а) можно брать любую из первообразных функций f(x) записываются в общем виде F(x) + С. Но принято применять ту первоначальную для которой С = 0.

По приведенному определению имеем:

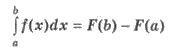
Эту формулу называют формулой Ньютона-Лейбница.

Заметим, что при исчислении определенных интегралов удобно разность F(b) - F(a) записывают так F(x) . Применяя это обозначение формулу Ньютона-Лейбница записывают еще и в таком виде:

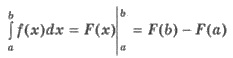
Рассмотрим примеры нахождения определений интегралов.

Пример 1. Вычислите интеграл sиn хdх.

Решения. Для функции f(х) = sin х одной из первообразных является F(х) = -cos х. Имеем по формуле Ньютона-Лейбница

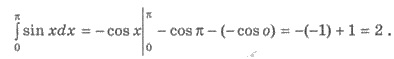
Пример 2. Вычислите интеграл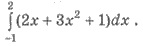

Решения. Сначала найдем первоначальную для функции f(х) = 2х + 3х² + 1. Используя правила вычисления первообразных и таблицу первообразных, имеем:

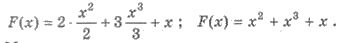
Получим

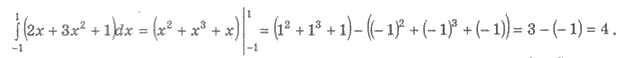
Заметим, что при оформлении этого примера нахождения первоначальной можно было не записывать отдельно. Тогда оформление приобретет следующий вид:

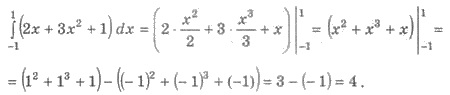
Пример 3. Вычислите интеграл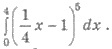

Решения. Используем правило 3 нахождения первообразных. Имеем