АЛГЕБРА И НАЧАЛА АНАЛИЗА

Раздел III. ФУНКЦИЯ

§22. ПЕРВОНАЧАЛЬНАЯ. ТАБЛИЦА ПЕРВООБРАЗНЫХ. ПРАВИЛА НАХОЖДЕНИЯ ПЕРВООБРАЗНЫХ.

4. Правила нахождения первообразных.

1) Если F - первообразная для f, a G - первообразная для g, то F + G - первообразная для f + g.

2) Если F - первообразная для f, а k - постоянная, то kF - первообразная для kf.

3) Пусть F(x) - первообразная для f(х), a k и b - некоторые постоянные, причем k ≠ 0. Тогда 1/k ∙ F(kx + b) - первообразная для функции f(kx + b).

Рассмотрим примеры использования этих правил.

Пример 1. Найдите общий вид первообразных для функций:

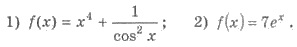
Решения.

1) Поскольку х⁵/5 первоначальная х⁴, a tg x - первообразная для 1/cos² x, то используя правило 1, получим общий вид первообразных для заданной функции:

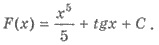
2) Поскольку е^х - первоначальная для еsup>х, то используя правило 2, получим общий вид первообразных для заданной функции F(х) = 7е^х + С.

Пример 2. Найдите общий вид первообразных для функции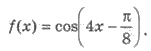

Решения. Для соs х одной из первообразных является sin х. Используя правило 3, получим общий вид первообразных для заданной функции:

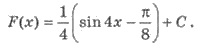
Пример 3. Для функции 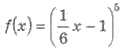найдите первоначальную F(x) такую, что F(12) = 3.

Решения. Используя правило 3 и тот факт, что одной из первоначальных для функции х⁵ есть x⁶/6 получим:

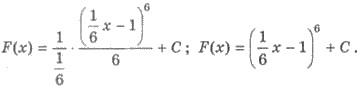
Поскольку F(12) = 3, то получим

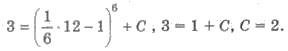
Итак, 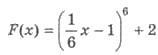- искомая первоначальная.