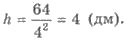АЛГЕБРА И НАЧАЛА АНАЛИЗА

Раздел III. ФУНКЦИЯ

§21. НАХОЖДЕНИЕ НАИБОЛЬШЕГО И НАИМЕНЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ НА ОТРЕЗКЕ. ПРИКЛАДНЫЕ ЗАДАЧИ НА НАХОЖДЕНИЕ НАИБОЛЬШЕГО И НАИМЕНЬШЕГО ЗНАЧЕНИЙ.

2. Прикладные задачи на нахождение наибольшего или (и) наименьшего значения некоторой величины.

При решении прикладных задач на нахождение наибольшего или (и) наименьшего значения некоторой величины можно использовать следующую схему:

1) Одну из величин обозначаем за х и по содержанию задачи накладываем ограничения на х.

2) Величину больше или (и) наименьшее значение которой требуется найти выражаем через х;

3) Находим наибольшее или (и) наименьшее значение полученной функции при наложенных ограничениях на х;

4) Выясняем какой практический смысл полученный результат.

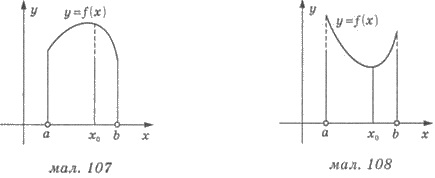
Заметим, что при решении некоторых практических задач необходимо найти больше или (и) наименьшее значение непрерывной функции на промежутке [а;b], а на интервале (а;b). Как правило, в таких случаях на интервале (а;b) функция имеет одну критическую точку. Если эта точка максимума, то именно в этой точке на интервале (а;b) функция имеет наибольшее значение (рис. 107), а если это точка минимума, то меньше (рис. 108).

Пример 1. Забором, длина которого 120 м, надо огородить огород наибольшей площади (рис. 109). Найдите размеры огорода.

Решения.

1) Обозначим через х м одну из двух параллельных сторон забора (рис. 110), тогда другая сторона будет равняться 120 - 2х (г), где 0 х 60.

2) Площадь огорода: S(x) = х(120 - 2х).

S(x) = 120х - 2x².

3) Найдем наибольшее значение функции:

S(x) = 120х - 2х² при условии х 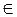(0;60).

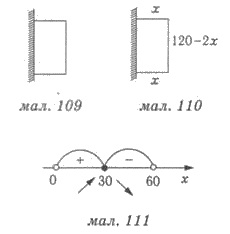
S'(x)= 120 - 2 ∙ 2x = 120 - 4x; S'(x) = 0, когда х = 30. Имеем х_mах = 30 (рис. 111).

4) Поскольку S(x) = 120 - 2х² непрерывна на (0;60) и имеет точку максимума х_mах = 30, то именно в этой точке S(x) достигает наибольшего значения. Следовательно, размер огорода 30 м и

120 - 2 ∙ 30 = 60 (м).

Пример 2. Необходимо изготовить открытый резервуар цилиндрической формы, объем которого равен 64π дм³. При каких размерах резервуара (радиусу основания и высоте) на его изготовление тратится наименьшее количество металла?

Решения.

1) Рассмотрим через r (дм) - радиус основания резервуара. Поскольку объем цилиндра V = πr²h, где h - высота, то имеем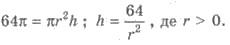

2) На изготовление резервуара расходуется такое количество металла 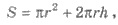πr² - площадь основания резервуара, 2πrh - площадь боковой поверхности. Так 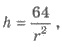то имеем

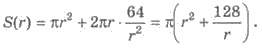
3) Найдем наименьшее значение функции 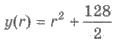при пусть r > 0.

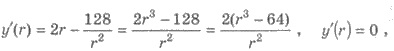когда r = 4. Имеем r_min = 4 (рис. 112).

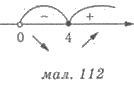
4) Поскольку 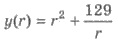непрерывная для r > 0 и имеет точку минимума r_min = 4, то именно в этой точке и в(r), а потому и S(r) достигает наименьшего значения. Следовательно, радиус основания цилиндра равен 4 дм, высота