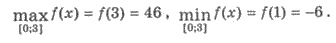АЛГЕБРА И НАЧАЛА АНАЛИЗА
Раздел III. ФУНКЦИЯ
§21. НАХОЖДЕНИЕ НАИБОЛЬШЕГО И НАИМЕНЬШЕГО ЗНАЧЕНИЯ ФУНКЦИИ НА ОТРЕЗКЕ. ПРИКЛАДНЫЕ ЗАДАЧИ НА НАХОЖДЕНИЕ НАИБОЛЬШЕГО И НАИМЕНЬШЕГО ЗНАЧЕНИЙ.
1. Нахождение наибольшего и наименьшего значения функции на отрезке.
В курсе математического анализа
доказывается теорема Вейєритрасса: непрерывная на отрезке [a;b] функция имеет на этом отрезке наибольшее и наименьшее
значение.
Эту теорему следует понимать так, что для
непрерывной на [a;b] функции
существуют точки отрезка [a;b] в
которых f(x) приобретает
наибольшего и наименьшего на [a;b] значения.
Если функция у= = f(x) непрерывна
на отрезке [а;b] и имеет на этом отрезке конечное
число критических точек, то она приобретает своего наибольшего и наименьшего значения
на этом отрезке или в критических точках, принадлежащих этому отрезку, либо на
концах отрезка.
Исходя из приведенного, можно
предложить следующую схему нахождения наибольшего и наименьшего значения
функции у = f(x) на промежутке [a;b]:
1) Проверяем вхождение заданного
промежутка в область определения функции.
2) Находим производную f '(x).
3) Находим критические
точки (внутренние точки области определения f(x), в которых f '(x) не
существует и решить уравнение f ‘(x) =
0.
4) Выбираем критические точки,
принадлежат промежутку [a;b].
5) Вычисляем значение
функции в выбранных критических точках и в точках а и b.
6) Сравниваем полученные
значение и находим наибольшее и наименьшее значения функции у = f(x) на промежутке [a;b].
7) Ответ.
Пример. Найдите наибольшее и
наименьшее значение функции
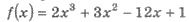на промежутке [0;3].
Решения.
1) D(f) = R, рассматриваемый промежуток принадлежит области определения.
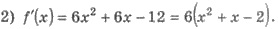
3) Производная существует во всех
точках; решение уравнения х2 +
х - 2 = 0, то х1 = 1; х2 = -2 - критические точки.
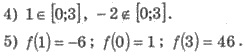
6) Следовательно, наибольшее значение функции
f(x) на заданном промежутке f(3) = 46, а
наименьшее - f(1) = -6.
7) Это записывают следующим образом:
