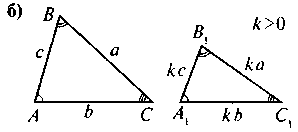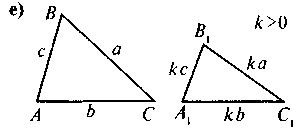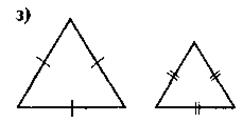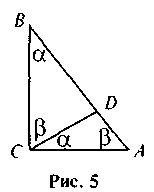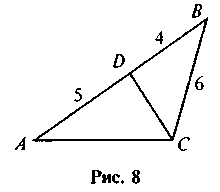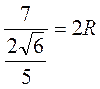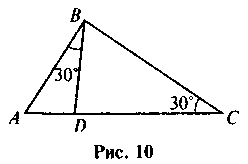|
Также на уроке следует проверить решение дополнительной задачи (полное решение этой задачи записывает на доске один из учеников заранее; учащиеся знакомятся с его содержанием после выполнения и проверки заданий математического диктанта).
III. Формулировка цели и задач урока На этом этапе урока уместными будут слова учителя о том, что на предыдущих трех уроках ученики отдельно изучали признаки подобия треугольников и способы их применения, причем каждого урока ученики решали задачи на применение лишь признаки той, которая изучалась на уроке, т.е. ученики работали в «искусственных условиях», при отсутствии проблемы выбора, когда заранее было известно, какой набор элементов треугольников (обусловлен определенной признаку подобия) следует выделить в данных треугольниках для доведения их сходства именно по определенному признаку. Учителю следует подчеркнуть, что на практике при решении задач, которые предусматривают применение признаков подобия треугольников, выбор определенного признака следует делать самому ученику, исходя из условия задачи и своих знаний. Поэтому для успешного решения задач на подобие треугольников ученикам, кроме устоявшихся знаний содержания отдельных признаков подобия треугольников и следствий из них, следует овладеть умениями выбирать признак или следствие согласно условия задачи. Итак, цель урока - закрепление и систематизация знаний учащихся о признаках подобия треугольников и отработки навыков их использования при решении задач на подобие треугольников.
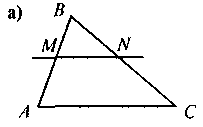
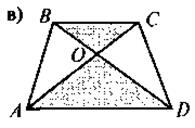
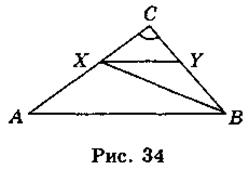
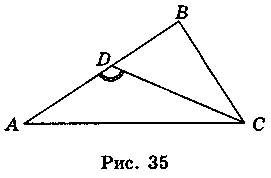
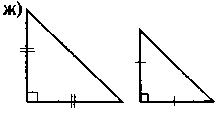
IV. Актуализация и систематизация опорных знаний Осознание, повторение и систематизация знаний учащихся о содержании определения и признаков подобия треугольников можно провести в такой форме: вниманию учащихся предлагается рис., по которым они выполняют задания - к каждому из рисунков составить соответствующее утверждение (определение или какую-то из признаков подобия треугольников). Для того, чтобы привлечь к работе как можно больше учащихся, можно организовать работу в малых Труппах. В таком случае сначала задание выполняется в группах, а затем результаты выполнения задания презентуются и корректируются.
Рис.
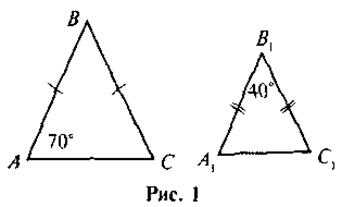
V. Отработка навыков Применение знаний в стандартных ситуациях 1. По данным рис. 1 докажите, что ΔАВС ~ ΔА1В1С1.
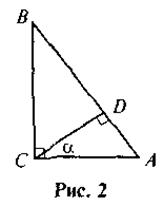
2. На рис. 2 найдите треугольники, подобные треугольника ABC, и докажите их подобие.
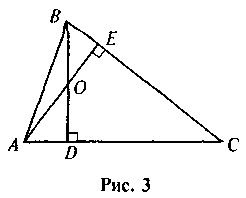
3. Найдите на рис. 3 все пары подобных треугольников и докажите их подобие.
4. По данным рис. 4 докажите, что ΔАВС ~ ΔА1В1С1.
5. На рис. 5 найдите треугольники, подобные треугольника ABC, и докажите их подобие.
6. На рис. 6 найдите все пары подобных треугольников и докажите их подобие.
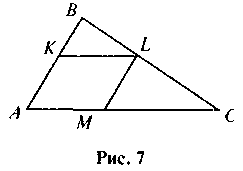
Применение знаний в нестандартных ситуациях 1. В треугольник ABC вписан ромб AKLM (рис. 7) Найдите периметр ромба, если ВК = 4 см, МС = 9 см. 2. Диагонали трапеции точкой пересечения делятся в отношении 3 : 7. Найдите основания трапеции, если ее средняя линя равна 10см
VI. Диагностика знаний и умений Учащимся предлагается самостоятельно решить задания как на знание и понимание признаков подобия треугольников, так и на применение этих знаний в комплексе с приобретенными ранее знаниями Самостоятельное решение задач 1. Найдите на рис. 8 подобные треугольники и докажите их подобие.
2. По данным рис. 9 докажите, что ΔАВС ~ ΔMBN.
3. Найдите на рис. 10 подобные треугольники и докажите их подобие.
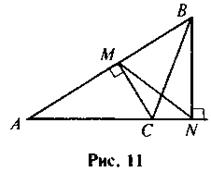
4. По данным рис. 11 докажите, что ΔABC ~ ΔANM.
5. Точка пересечения диагоналей трапеции делит одну из них на отрезки длиной 5 см и 9 см. Найдите основания трапеции, если их сумма равна 70 см. 6. Основы трапеции равны 7 см и 15 см. Найдите отрезки диагонали, на которые ее делит вторая диагональ, если разность этих отрезков равна 24 см.
VII. Итоги урока По окончании выполнения самостоятельных заданий проводится проверка правильности выполнения, таким образом устанавливается, достигнута мста урока; у учеников появляются основания для самооценки и осознания своих недостатков, над которыми следует работать.
VIII. Домашнее задание Повторить содержание: определение, признаки подобия треугольников и опорные факты для доказательства подобия треугольников; содержание понятия перпендикуляра к прямой; определение и свойства прямоугольного треугольника. Решить задачи. 1. В рівнобедреному треугольнике ABC с основанием АС угол В равен 36°, AD - биссектриса треугольника. Докажите, что ΔАВС ~ ΔCAD. 2. Одна из диагоналей трапеции равна 28 см и делит другую диагональ на отрезки длиной 5 см и 9 см. Зная, что меньшее основание трапеции равно 6 см, найдите: а) отрезки, на которые точка пересечения диагоналей делит первую диагональ; б) боковую основу трапеции. 3. В треугольник ABC вписан ромб АКРЕ так, что угол А общий, а вершина Г принадлежит стороне ВС. Найдите сторону ромба, если АВ = 6 см, АС = 3 см.
|
| ||||||||||||||||||||||||||||||||||||