Урок № 30
Тема. Подобие треугольников по трем сторонам
Цель: добиться понимания учащимися содержания признаки подобия треугольников по трем сторонам, плана их доведения. Формировать умения:
· воспроизводить содержание изученного признака;
· выделять в треугольниках элементы для определения их сходства по трем сторонам;
· применять формулировку третьего признака подобия треугольников для решения задач.
Тип урока: усвоение новых знаний.
Наглядность и оборудование: конспект «Подобие треугольников».
Ход урока
I. Организационный этап
II. Проверка домашнего задания
Во время устного обсуждения контрольных моментов задач домашней работы ученики должны воспроизвести аргументированные рассуждения с использованием определения и изученных признаков подобия треугольников.
III. Формулировка цели и задач урока
Поскольку подходы к доведению всех трех признаков подобия треугольников одинаковы, то схемы проведения уроков по изучению признаков подобия треугольников тоже похожи.
Ученикам предлагаем ответить на вопросы:
1. Какие два треугольника называются равными?
Можно доказать, используя определение равных треугольников, треугольники, изображенные на рис. 1, являются равными? Какое утверждение можно для этого использовать?
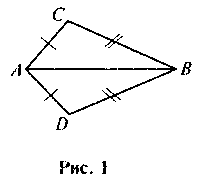
2. Какие два треугольника называются подобными? Можно доказать, используя определение подобных треугольников, треугольники, изображенные на рис. 2, являются подобными? Или известное вам утверждение, которое можно было бы для этого использовать?
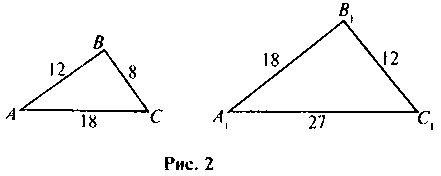
Выполнение задания опять подводит учащихся к соображений, аналогичных тем, что имели место на предыдущих двух уроках:
· определение подобия треугольников имеет определенные ограничения в применении;
· изучены на предыдущих двух уроках признаки подобия треугольников (по двум углами и двумя сторонами и углом между ними) имеют ограниченный круг применения;
· несмотря на существование определенных аналогий между понятием равенства и подобия треугольников и на существование признаков равенства треугольников, допускает существование другого, кроме изученных, признаки подобия треугольников (похожа по набору элементов на признак равенства треугольников по трем сторонам).
Изучение этого признака подобия треугольников и овладение умениями использовать ее при решении задач составляет цель урока.
IV. Актуализация опорных знаний
С целью успешного усвоения учащимися признаки подобия треугольников по трем сторонам, а также идеи ее доведения, ученикам следует активизировать знания и умения относительно признаков равенства треугольников; свойства соответствующих углов при параллельных прямых и секущей; признаки подобия треугольников по двум углам.
Выполнение устных упражнений по готовым рисункам
1 |
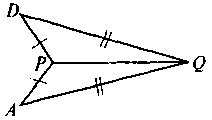
|
Дано: AP = DP, AQ = DQ.
Доказать: ΔPAQ = ΔPDQ |
2 |
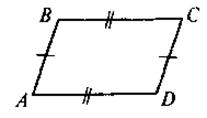
|
Дано: AB = CD, AD = BC.
Доказать:  A = A =  C C |
3 |
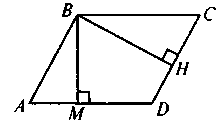
|
Дано: ABCD - параллелограмм, ВМ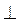 AD, BH AD, BH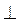 CD. CD.
Доказать: 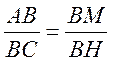 |
4 |
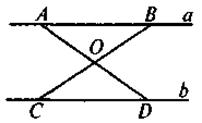
|
Дано: а || b, А и В - произвольные точки. Доказать: 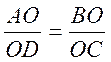 |
V. Усвоение знаний
План изучения нового материала
1. Теорема (признак подобия треугольников по трем сторонам): формулировка и доказательство.
2. Примеры применения.
@ Все замечания относительно особенностей способа изучения признаков подобия треугольников, которые были сделаны ранее, имеют место и на этом уроке:
· доведение признаки подобия треугольников по трем сторонам проводится с ссылкой на свойства соответствующих углов при параллельных прямых и секущей, на третий признак равенства треугольников и признак подобия треугольников по двум углам;
· пониманию доведение признаки подобия треугольников по трем сторонам способствует выполнение устных упражнений на повторение (см. выше);
· с целью облегчения запоминания доведение рекомендуется составить план, который впоследствии ученики зафиксируют в тетрадях. Закрепление содержания доказанной теоремы проводится во время выполнения устных упражнений.
VI. Формирование умений
Выполнение устных упражнений
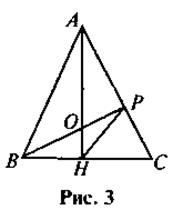
1. АН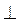 ВС, BP
ВС, BP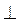 АС (рис. 3).
АС (рис. 3).
1) Назовите подобные треугольники.
2) Найдите ВС, если АН = 2, ВС = 8, АС = 5.
2. В треугольниках ABC и А1В1С1 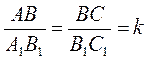 .
.
Которую равенство необходимо добавить условия, чтобы можно было доказать подобие этих треугольников? Назовите все возможные варианты ответа.
3. Даны треугольники ABC и KMN, в которых 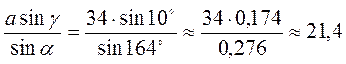 . Назовите угол треугольника KMN, что равен углу С. Почему эти углы равны?
. Назовите угол треугольника KMN, что равен углу С. Почему эти углы равны?
Выполнение письменных упражнений
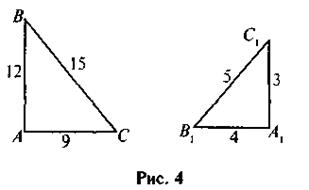
1. По данным рисунка 4 докажите подобие треугольников ABC и А1В1С1.
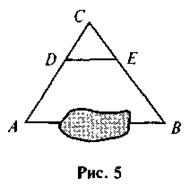
2. Определите расстояние от точки А до недоступной точки В (рис. 5), если СА = 60 м, СВ = 90 м, CD = 20 м, СЕ = 30 м, DE = 40 м. Проведите необходимые доказательства.
3. Определите, подобны ли треугольники со сторонами: 15, 12, 13 и 26, 24, 30.
4. На рисунке 6 найдите подобные треугольники и докажите их подобие.

@ Соображения, лежащие в основе доказательства подобия треугольников по трем сторонам, строятся по традиционной схеме.
Рассмотрим треугольники... и... В них: (дается полный перечень пар равных отношений соответствующих сторон в отношении признаки подобия), поэтому треугольники... и... подобны по трем сторонам.
VII. Итоги урока
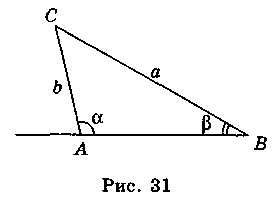
Какие условия следует добавить, чтобы изображенные на рис. 7 треугольники были подобными:
а) за двумя сторонами и углом между ними;
б) по трем сторонам?
VIII. Домашнее задание
Изучить содержание и доказательства теоремы, повторить содержание признаков подобия треугольников.
Решить задачи.
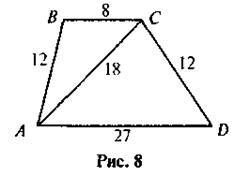
1. На рисунке 8 найдите подобные треугольники и докажите их подобие.
2. В треугольнике ABC точка О является центром описанной окружности, точки A1, В1, С1 являются серединами отрезков ОА , ОВ, ОС соответственно. Докажите, что треугольники ABC и А1В1С1 подобные.

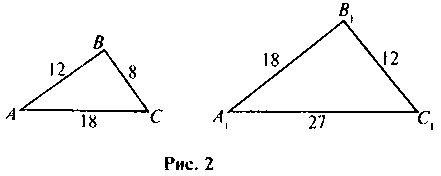



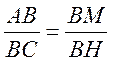

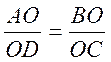

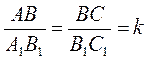 .
.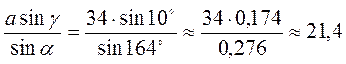 . Назовите угол треугольника
. Назовите угол треугольника 



