Урок 31

Тема. Перпендикуляр и наклонная. Взаимосвязь между длинами наклонных, проведенных из одной точки, и длины их проекций

Цель урока: формирование понятий: перпендикуляр к плоскости, наклонная, основание наклонной, основание перпендикуляра, проекции наклонной на плоскость, расстояния от точки до плоскости. Выявление взаимосвязи между длинами двух наклонных, проведенных из одной точки к плоскости, и длины их проекций.

Оборудование: стереометрический набор.

Ход урока

И. Проверка домашнего задания

1. Два ученика воспроизводят на доске решение задач № 14, 15.

2. Решение задач.

1) Даны плоскость α, перпендикулярную к ней прямую а и другую прямую b, не лежащая в плоскости α. Укажите, какие из приведенных утверждений правильные, а какие - неправильные:

а) если b || a, то bα;

б) если bα , то b || а ;

в) если bα, то а и b скрещивающиеся;

г) если bα, то а и b пересекаются.

2) Даны плоскость α, параллельную ей прямую а и некоторую прямую b, не лежащая в плоскости α. Укажите, какие из приведенных утверждений правильные, а какие - неправильные:

а) если b || a, то обязательно b || α;

б) если bα, то обязательно bа;

в) если bα и b пересекает а, то bа;

г) если bα, то b и а обязательно скрещивающиеся.

3. Обсуждение правильности выполнения учащимися задач № 14, 15.

II. Восприятие и осознание нового материала

Перпендикуляр и наклонные, взаимосвязь между длинами похилих. проведенных из одной точки, и длины их проекций

Перпендикуляром, опущенным из данной точки на данную плоскость, называется отрезок прямой, перпендикулярной к плоскости, что содержится между данной точкой и плоскостью.

На рис. 162 прямая AC перпендикулярна к плоскости α и пересекает ее в точке С, следовательно, отрезок AC - перпендикуляр, опущенный из точки А на плоскость α. Конец этого отрезка, лежащий в плоскости, то есть точка С, называется основанием перпендикуляра.

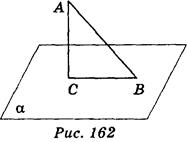
Если AC - перпендикуляр к плоскости α, а точка В - отличная от С точка этой плоскости, то отрезок АВ называют наклонной, проведенной из точки А на плоскость α. Точка В - основание наклонной. Отрезок, соединяющий основания перпендикуляра и наклонной, проведенных из одной и той же точки, называется проекцией наклонной. На рис. 162 отрезок ВС - проекция наклонной АВ на плоскость α.

Примерами материальных моделей перпендикуляров являются: столбы, телевизионные башни и др.

Решение задач

1. Найти длину наклонной, если длина перпендикуляра равна 4 см, а проекция наклонной на плоскость - 3 см.

2. Найти проекцию наклонной на плоскость, если наклонная равна 13 см, а перпендикуляр, проведенный из той же точки,- 12 см.

3. Найти длину перпендикуляра, если наклонная равна 10 см, а ее проекция на плоскость - 8 см.

4. Сколько перпендикуляров можно опустить из данной точки к данной плоскости? Почему?

5. Сколько наклонных можно провести из данной точки к данной плоскости?

6. Как следует установить на крестовине елку, чтобы она была перпендикулярна к плоскости пола?

7. Как на практике с помощью отвеса проверить вертикальность установленного столба?

Следует отметить, что перпендикуляр, опущенный из точки, короче любой наклонной, проведенной через данную точку.

Расстоянием от точки до плоскости называется длина перпендикуляра, опущенного из этой точки на плоскость.

Решение задач

1. Найти расстояние от точки А до граней куба, если ребро куба равно 10 см (рис. 163).

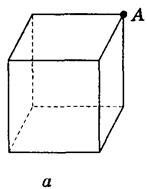
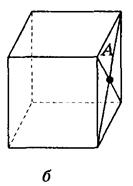
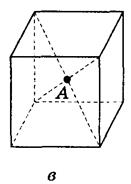
Рис. 163

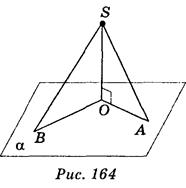
2. Из точки S проведен к плоскости а перпендикуляр SO и наклонные SA и SB. Длины наклонных соответственно равны 13 и 20 см. Длина проекции наклонной AS равна 5 см (рис. 164). Найти расстояние от точки S до плоскости и длину проекции наклонной SB.

Изучение взаимосвязи между длинами наклонных, проведенных из одной точки, и длинами их проекции уместно провести путем решения задач.

Задача.

Из некоторой точки проведены к плоскости две наклонные и перпендикуляр. Докажите, что если:

1) наклонные равны, то равны и их проекции;

2) проекции наклонных равны, то равны и наклонные.

3) наклонные неровные, то большая наклонная имеет большую проекцию.

Доведение

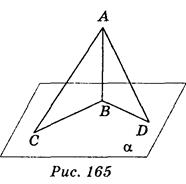
Пусть АВα (рис. 165); AC и AD - наклонные; AC > BD.

С ΔAСВ AC = .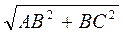

Из ΔАDB AD = .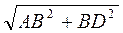

Согласно условию AC > AD , тогда

> ;

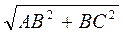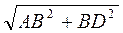АВ2 + ВС2 > АВ2 + BD2, или ВС2 > BD2; следовательно, ВС > BD.

4) Докажите: если наклонные неровные, то большей проекции соответствует большая наклонная.

III. Закрепление и осмысление знаний учащихся

Решение задач

1. Задача № 22 из учебника (с. 36).

2. Задача № 23 из учебника (с. 36).

Решение

Пусть АВα (рис. 165); AC = 17 см, AD = 10 cm, СB - BD = 9 cm. Пусть BD = x cm, тогда CB = (x + 9) cm.

Из ΔАВD: АВ2 = AD2 - BD2 = 100 - x2.

Из ΔАСВ: АВ2 = AC2 - BC2 = 289 - (x+ 9)2. Тогда 100 - x2 = 289 - (x + 9)2; 100 - x2 = 289 - x2 - 18x - 81; 18x = 108; x = 6.

Следовательно, BD = 6 cm, CB = 6 + 9 = 15 (см).

Ответ. 6 см и 15 см.

3. Задача № 25 из учебника (с. 36).

Решение

Пусть АВα (рис. 165); AD = 23 см, AC = 33 см, BD : CB = 2 : 3.

Пусть BD = 2x см, CB = 3х см. Из ΔАВD: АВ2 = AD2 - BD2 = 232 - 4x2.

Из ΔАВС: АВ2 = AC2 - BC2 = 332 - 9x2. Тогда 232 - 4x2 = 332 - 9x2;

5x2 =332 - 232; 5x2 = (33 - 23)(33 + 23); x2 =112 и АВ = 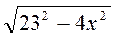= = 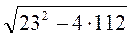= 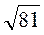9 (см). Следовательно, длина перпендикуляра равна 9 см.

Ответ. 9 см.

IV. Домашнее задание

§3, п. 18; контрольные вопросы № 7-9; задача № 24 (с. 36).

V. Подведение итога урока

Вопрос к классу

1) Что такое перпендикуляр, опущенный из данной точки к плоскости?

2) Что такое наклонная, проведенная из данной точки к плоскости?

3) Сколько перпендикуляров и наклонных можно построить из данной точки к плоскости?

4) 3 данной точки к плоскости проведены две наклонные. Что можно утверждать о проекции наклонных на плоскость, если наклонные:

а) уровне;

б) не равны?