Урок 30
Тема. Свойства прямой и плоскости, перпендикулярных между собой
Цель урока: формирование знаний учащихся о свойства перпендикулярных прямых и плоскостей.
Оборудование: стереометрический набор, схема «Свойства прямо и плоскости, перпендикулярных между собой» (с. 116).
Ход урока
И. Проверка домашнего задания
1. Коллективное обсуждение решения задачи № 10.
2. Математический диктант.
Дано изображение куба: вариант 1 - рис. 151, вариант 2 - рис. 152.
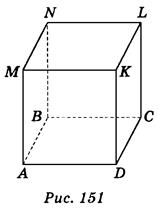
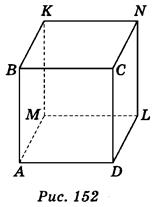
Пользуясь изображением, запишите:
1) плоскость, которая проходит через точку М прямой AM и перпендикулярна к ней; (2 балла)
2) прямую, которая перпендикулярна к плоскости АВС и проходит через точку D; (2 балла)
3) прямую, которая перпендикулярна к плоскости АВС и проходит через точку N; (2 балла)
4) плоскость, которая перпендикулярна к прямой BD; (2 балла)
5) прямые, перпендикулярные к плоскости АМС; (2 балла)
6) плоскости, которые перпендикулярны к прямой DC. (2 балла)
Ответ.
Вариант 1. 1) (MNK); 2) KD; 3) BN; 4) (АСМ); 5) BD и KN; 6) (ADK) и (BCL).
Вариант 2. 1) (MNK); 2) DL; 3) CN; 4) (АСМ); 5) BD i KL; 6) (BCN) и (ADM).
II. Восприятие и осознание нового материала
Свойства прямой и плоскости, перпендикулярных между собой
Теорема 1.
Если плоскость перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и ко второй.
Доведение
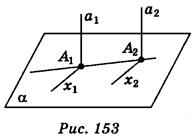
Пусть а1 || а2 и a1 α. Докажем, что α
α. Докажем, что α а2 (рис. 153). Точки А1 и А2 - точки пересечения а1 и а2 с плоскостью α.
а2 (рис. 153). Точки А1 и А2 - точки пересечения а1 и а2 с плоскостью α.
В плоскости α через точку А2 проведем произвольную прямую х2, а через точку А1 - прямую х1 такое, что х1 || х2. Поскольку a1 || a2, x1 || x2 и а1 х1, то по теореме 3.1 а2
х1, то по теореме 3.1 а2 х2. Поскольку х2 выбрана произвольно в плоскости α, то а2
х2. Поскольку х2 выбрана произвольно в плоскости α, то а2 α.
α.
Теорема 2.
Если две прямые перпендикулярны к одной и той же плоскости, то данные прямые параллельны.
Доведение
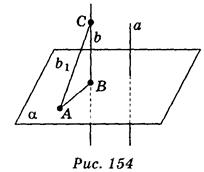
Пусть a α, b
α, b α. Докажем, что а || b (рис. 154). Предположим, что а
α. Докажем, что а || b (рис. 154). Предположим, что а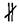 b. Тогда через точку С прямой b проведем b1 , параллельную а. А поскольку
b. Тогда через точку С прямой b проведем b1 , параллельную а. А поскольку α, то и b1
α, то и b1 α по доказанной теореме, а по условию b
α по доказанной теореме, а по условию b α. Если точки А и В - точки пересечения прямых b1 и b с плоскостью α, то из предположения следует, что в треугольнике
α. Если точки А и В - точки пересечения прямых b1 и b с плоскостью α, то из предположения следует, что в треугольнике  A =
A =  В = 90°, что не может быть. Следовательно, а || b.
В = 90°, что не может быть. Следовательно, а || b.
Решение задач
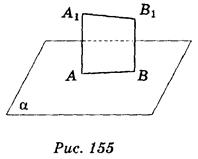
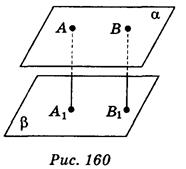
1. Определите вид четырехугольника AA1B1B если:
а) АА1 α; АА1 || ВВ1; А
α; АА1 || ВВ1; А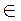 α, В
α, В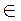 α; AA1 ≠ ВВ1 (рис. 155);
α; AA1 ≠ ВВ1 (рис. 155);
б) АА1 α; ВВ1
α; ВВ1 α;
α; 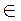 α, В
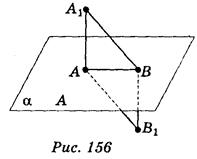
α, В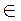 α (рис. 156);
α (рис. 156);
в) 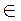 α;
α; 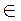 α; АА1
α; АА1 α; ВВ1
α; ВВ1 α; АА1 = ВВ1 (рис. 156).
α; АА1 = ВВ1 (рис. 156).
2. Задача № 12 из учебника (с. 35).
3. Задача № 13 из учебника (с. 35).
4. Задача № 16 из учебника (с. 35).
Теорема 3.
Если прямая перпендикулярна к одной из двух параллельных плоскостей, то она перпендикулярна и ко второй.
Доведение
Пусть α || β, а α. Докажем, что α
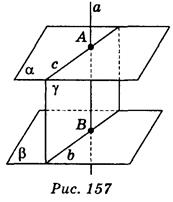
α. Докажем, что α β. (рис. 157). Пусть точки А и В - точки пересечения прямой а с плоскостями α и β. В плоскости β проведем через точку В произвольную прямую b. Через прямую b и точку А проведем плоскость γ, которая пересекает α по прямой с, причем с || b. А поскольку
β. (рис. 157). Пусть точки А и В - точки пересечения прямой а с плоскостями α и β. В плоскости β проведем через точку В произвольную прямую b. Через прямую b и точку А проведем плоскость γ, которая пересекает α по прямой с, причем с || b. А поскольку α , то а
α , то а с (по определению прямой, перпендикулярной к плоскости). Так а
с (по определению прямой, перпендикулярной к плоскости). Так а с, b || с и а, b, с лежат в γ, то а
с, b || с и а, b, с лежат в γ, то а b. Учитывая, что b - произвольная прямая плоскости β, имеем а
b. Учитывая, что b - произвольная прямая плоскости β, имеем а β.
β.
Теорема 4.
Если две плоскости, перпендикулярные к одной и той же прямой, то они параллельны.
Доведение
Пусть α а β
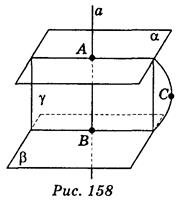
а β а, докажем, что α || β (рис. 158). Пусть точки А и В - точки пересечения прямой а с плоскостями α и β. Предположим, что α
а, докажем, что α || β (рис. 158). Пусть точки А и В - точки пересечения прямой а с плоскостями α и β. Предположим, что α 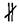 β. Возьмем точку С на прямой пересечения плоскостей α и β. С
β. Возьмем точку С на прямой пересечения плоскостей α и β. С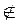 а, ибо в противном случае через точку С проходили бы две различные плоскости α и β, перпендикулярные к прямой а, что невозможно. Проведем плоскость γ через точку С и прямую а, эта плоскость пересекает α и β по прямым АС и ВС соответственно. А поскольку
а, ибо в противном случае через точку С проходили бы две различные плоскости α и β, перпендикулярные к прямой а, что невозможно. Проведем плоскость γ через точку С и прямую а, эта плоскость пересекает α и β по прямым АС и ВС соответственно. А поскольку α, то а
α, то а АС, аналогично а
АС, аналогично а ВС. Следовательно, в плоскости α через точку С проходят две различные прямые АС и ВС, перпендикулярные к прямой а, что невозможно. Следовательно, α || β.
ВС. Следовательно, в плоскости α через точку С проходят две различные прямые АС и ВС, перпендикулярные к прямой а, что невозможно. Следовательно, α || β.
Решение задач
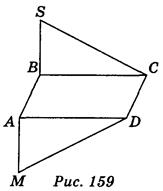
1. Пусть ABCD - прямоугольник, BS АВ, AM
АВ, AM АВ (рис. 159). Как расположены плоскости AMD и BSC?
АВ (рис. 159). Как расположены плоскости AMD и BSC?
2. В1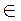 β; АА1
β; АА1 α, АА1
α, АА1 β; BВ1 || АА1; АА1 = 12 cm, A1B = 13 см (рис. 160). Найти АВ.
β; BВ1 || АА1; АА1 = 12 cm, A1B = 13 см (рис. 160). Найти АВ.
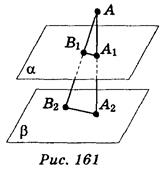
3. А1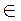 α; В1
α; В1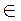 α, А2
α, А2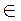 β, 2
β, 2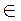 β, AA1
β, AA1 α; α || β (рис. 161). Определите вид треугольников AA1B1 и АА2В2
α; α || β (рис. 161). Определите вид треугольников AA1B1 и АА2В2
III. Домашнее задание
§3, п. 17; контрольные вопросы № 5, 6; задачи № 14, 15 (с. 35).
IV. Подведение итога урока
При подведении итога урока можно воспользоваться данной схемой.
Свойства прямой и плоскости, перпендикулярных между собой |
|
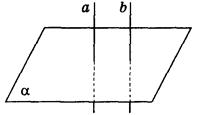
Дано:
а || b,
a α. α.
Доказать:
b a. a. |
Дано:
a α, α,
b α. α.
Доказать:
а || b. |
|
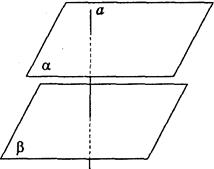
Дано:
α || β,
а α. α.
Доказать: β  а. а. |
Дано:
α a . a .
β a. a.
Доказать:
α || β. |
Вопрос к классу
1) Как расположены прямые, перпендикулярные к плоскости?
2) Как расположены в пространстве плоскости, которые перпендикулярны к прямой?
3) Как расположены прямая и плоскость, если параллельная прямая к данной прямой перпендикулярна к плоскости?
4) Как расположены прямая и плоскость, если плоскость, параллельная данной плоскости, перпендикулярна к данной прямой?












