АЛГЕБРА И НАЧАЛА АНАЛИЗА

Раздел III. ФУНКЦИЯ

§18. ГЕОМЕТРИЧЕСКИЙ И ФИЗИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ.

1. Геометрический смысл производной.

Геометрический смысл производной заключается в следующем: угловой коэффициент касательной к графику функции у = f(x), которая приведена в точке этого графика с абсциссой х₀ равен производной функции у = f(x) в этой точке (рис. 96), то есть

k = f '(x₀).

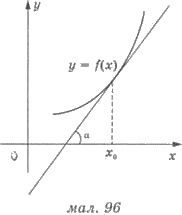
Поскольку k = tg α, где α - угол, который образует касательная с положительным направлением оси абсцисс, то в случае f '(x₀) > 0, угол α - острый, если f '(x₀) = 0, то касательная параллельна оси абсцисс (или совпадает с ней), а в случае f '(x₀) 0, угол α - тупой.

Пример 1. Найдите угловой коэффициент касательной, проведенной к графику функции f(х) = х² в точке с абсциссой х₀ = -1.

Решения. k = f '(-1). Поскольку f '(x) = (х²) = 2х, то k = 2 ∙ (-1) = -2.

Пример 2. Найдите угол наклона к оси абсцисс касательной, проведенной к графика функции f(х) = 2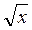, что проведенная в точке А(1; 2).

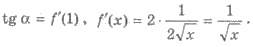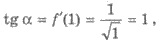Решения. Тогда a поэтому α = π/4.

Пример 3. На графике функции 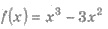найдите такие точки, в которых касательная, проведенная к графику функции, параллельная оси абсцисс.

Решения. Пусть х₀ - абсцисса искомой точки. Тогда, исходя из условия f(х₀) = 0, имеем: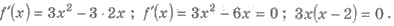

Находим x₀ = 0 или х₀ = -2. Следовательно, учитывая, 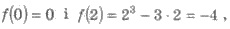такими точками являются точки (0;0) и (2;-4).