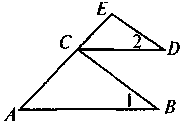Урок № 29
Тема. Подобие треугольников с двумя сторонами и углом между ними
Цель: добиться понимания учащимися содержания второй признаки подобия треугольников и плана ее доведения. Формировать умения:
· воспроизводить содержание изученного признака;
· выделять в треугольниках элементы для определения их сходства за двумя сторонами и углом между ними;
· применять формулировку второго признака подобия треугольников к решению задач.
Тип урока: усвоение новых знаний.
Наглядность и оборудование: конспект «Подобие треугольников».
Ход урока
I. Организационный этап
II. Проверка домашнего задания
Решение домашних задач подается на доске в виде готовых рисунков с комментариями, в которых некоторые фрагменты пропущены. Учащиеся должны заполнить пропуски соответствующими записями. Эту работу можно провести как самостоятельную и наиболее удачное исполнение оценить.
III. Формулировка цели и задач урока
Учитывая то, что содержание материала урока определенным образом связан с материалом предыдущего урока, то можно применять те же самые приемы, что и на предыдущем (с коррекцией на содержание материала данного урока). А именно предлагаем учащимся ответить на вопрос.
1. Какие два треугольника называются равными? Можно доказать, используя определение равных треугольников или признак равенства треугольников по стороной и двумя прилежащими к ней углами, что треугольники, изображенные на рис. 1, являются равными? Какое утверждение можно для этого использовать?
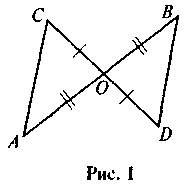
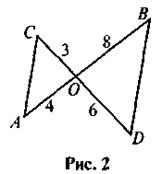
2. Какие два треугольника называются подобными? Можно доказать, используя определение подобных треугольников или признак подобия треугольников по двум углам, что треугольники, изображенные на рис. 2, являются подобными? Или известное вам утверждение, которое можно было бы для этого использовать?
Ответы на вопросы помогают учащимся осознать, что, во-первых, так же, как и определение равенства треугольников, определение подобия треугольников имеет определенные ограничения в применении; во-вторых, признак подобия треугольников по двум углам (так же, как и признак равенства треугольников по стороной и двумя прилежащими к ней углами) имеет также ограниченный круг применения; в-третьих, несмотря на существование определенных аналогий между понятием равенства и подобия треугольников и признаков равенства треугольников, можно предположить, что существует другая, кроме изученной на предыдущем уроке, признак подобия треугольников (похожа по набору элементов на признак равенства треугольников с двумя сторонами и углом между ними). Изучение этого признака подобия треугольников и овладение умениями использовать ее при решении задач составляет цель урока.
IV. Актуализация опорных знаний
Для успешного усвоения учащимися признаки подобия треугольников за двумя сторонами и углом между ними, а также идеи ее доведения, ученикам следует активизировать знания и умения относительно признаков равенства треугольников, свойства углов при параллельных прямых и секущей, применение теоремы о пропорциональные отрезки, определение подобных треугольников и признаки подобия треугольников по двум углам.
Выполнение устных упражнений по готовым рисункам
1 |
|
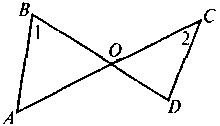
Дано:  1 = 1 =  2. 2.
Доказать: ΔАВО ~ ΔDCO |
2 |
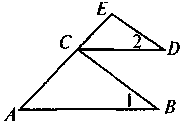
|
Дано: АВ || CD,  1 = 1 =  2. 2.
Доказать: ΔABC ~ ΔCDE |
3 |
|
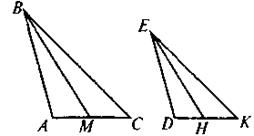
Дано: ΔАВС ~ ΔDEK,
М, Н - середины АС и DK.
Доказать: ΔВМС ~ ΔЕНК |
V. Усвоение знаний
План изучения нового материала
1. Теорема (признак подобия треугольников за двумя сторонами и углом между ними): формулировка и доказательство.
2. Примеры применения второго признака подобия треугольников.
@ Так же как и признак подобия треугольников по двум углам признак подобия треугольников за двумя сторонами и углом между ними приходится не через преобразование подобия (как это было ранее), а со ссылками на равенство соответствующих углов при параллельных прямых и секущей, на признак подобия треугольников по двум углам и определение подобных треугольников. Следовательно, если на предыдущем этапе урока должным образом была проведена подготовительная работа, то доведение признаки подобия треугольников за двумя сторонами и углом между ними должно быть понятным для учеников, а потому воспроизведения доказывания (как это требует программа) не составит для учащихся трудностей (для облегчения запоминания доведение рекомендуется составить план, который впоследствии ученики зафиксируют в тетрадях). Закрепление содержания доказательство теоремы проводится во время выполнения устных упражнений (см. ниже).
VI. Формирование умений
Выполнение письменных упражнений
1. По данным рисунка 3 докажите подобие треугольников ABC и А1В1С1.
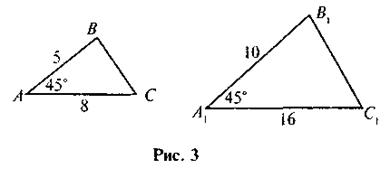
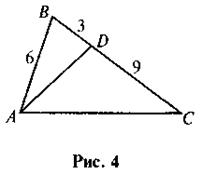
2. На рисунке 4 найдите подобные треугольники и докажите их подобие.
3. На одной стороне нераскрывшегося угла А отложены отрезки ОА = 9 см и ОВ = 12 см. а на другой стороне - отрезки ОС = 6 см и OD = 18 см. Или подобные треугольники ОАС и ВBD? Или подобные треугольники ОВС и ODA?
@ Во время решения задач продолжается работа по формированию умений учащихся выполнять построение доказательства сходства в форме, которая наилучшим образом соответствует утверждению признаки, изученной на уроке. Эта форма может быть записана учениками в виде трафарета.
Рассмотрим треугольники... и ... В них:
(дается полный перечень элементов этих треугольников с обоснованием согласно признаки подобия треугольников за двумя сторонами и углом между ними), поэтому треугольники... и ... подобные за двумя сторонами и углом между ними.
VII. Итоги урока
Какие условия следует добавить, чтобы изображенные на рис. 5 треугольники были подобными:
а) за двумя углами;
б) за двумя сторонами и углом между ними?
VIII. Домашнее задание
Изучить содержание и доведение теорема (признак подобия треугольников за двумя сторонами и углом между ними).
Решить задачи.
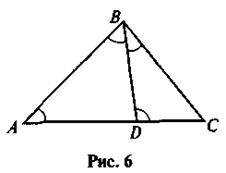
1. На рисунке 6 найдите подобные треугольники и докажите их подобие.
2. Через точку на стороне произвольного треугольника необходимо провести прямую, которая отсекает от данного треугольника подобный треугольник. Сколькими способами это можно сделать? Как изменится ответ, если в условии задачи вместо произвольного треугольника рассмотреть равнобедренный; равносторонний? Проведите исследование.
3. Известно, что треугольники ABC и МРК удовлетворяют условиям: АВ = 2 см, ВС = 4 см, АС = 3 см, MP = 6 см, МК = 9 см,  A =
A =  M. Найдите длину стороны РК.
M. Найдите длину стороны РК.
4. Отрезки АВ и CD пересекаются в точке О. Известно, что АО = 15 см, OD = 5 см, СО : ОВ = 1 : 3, AB + CD = 24 см. Найдите длины отрезков АВ и CD.